How can we solve this task in SMath?
3-mass.pdf (313 KiB) downloaded 90 time(s).

I decided to have some fun by trying to solve this using only SMath basic capabilities. I found it easier to turn everything upside-down (i.e. to pretend that gravity pulled up instead of down!) and only reverted to the normal view when plotting the position graphs.
I used an ultra-simple approach based on getting three sets of guesses for each mass coordinate and iterating until their differences were smaller than my specified tolerance. It’s crude, but it worked!
Life would be much simpler of course if SMath had its own minimize or maximize function.


3_weights_stvmath.sm (37 KiB) downloaded 66 time(s).

>Life would be much simpler of course if SMath had its own minimize or maximize function...

...with constrains.

Posted 

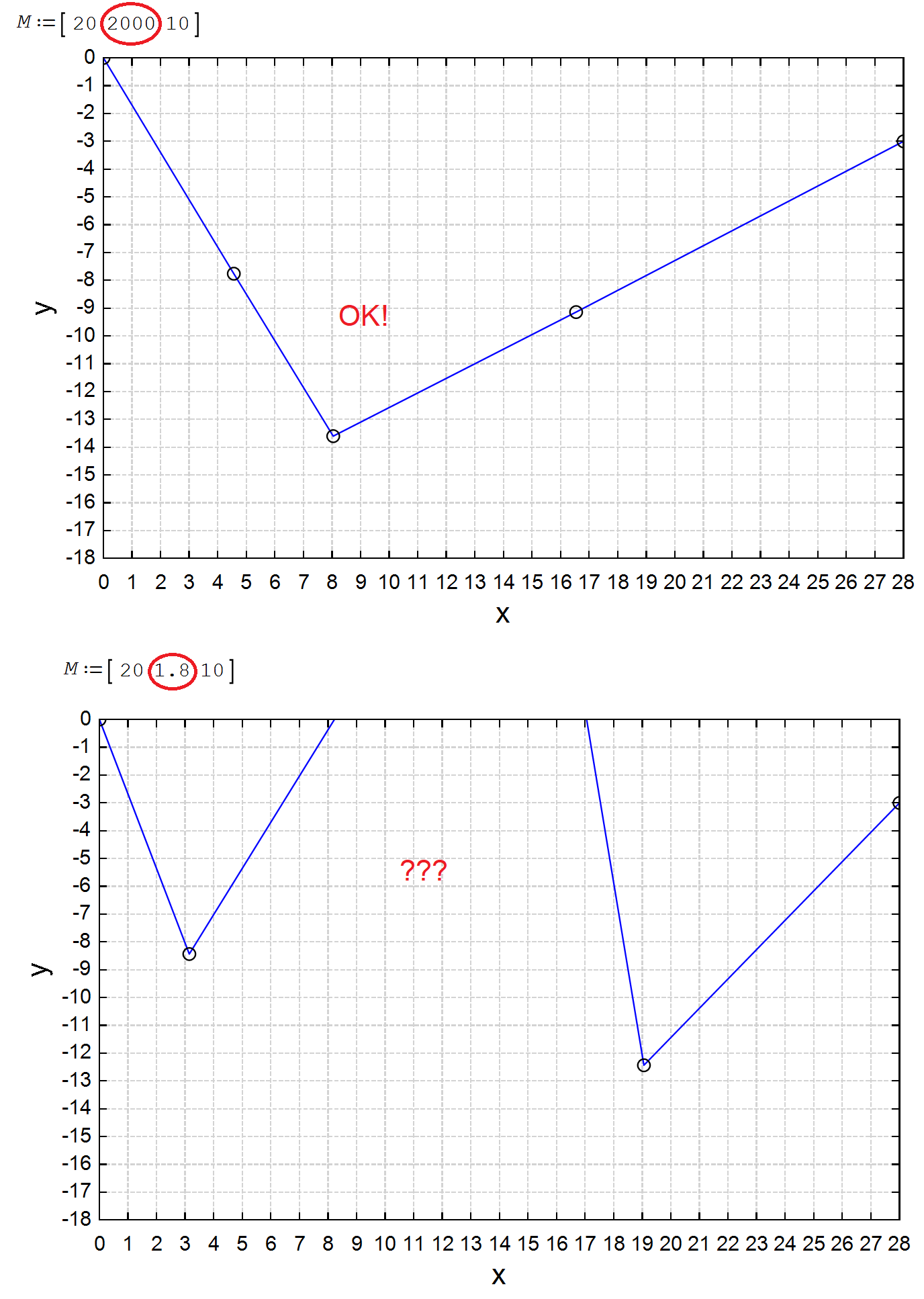
Yes. In the loop where it checks for unacceptable y2 values I should have added the line, msg:="Unacceptable y2 values. Try different initial guesses".
Additionally, by changing lambda = lambda/2 to lambda = -lambda, it seems to work ok!
If you change the initial guess for y2 to 11.5 it also works ok.


Note: The method is very crude. It won't work for more than three weights, for example, without significant modification.

I'm still playing with this example!

The attached uses a force-based approach, rather than an energy=based one.

I couldn't figure out how to use the in-built Jacobian functions for my forces function, so had to construct it by hand (luckily, it's a very simple task here).

3_weights_stvmath_b.sm (38 KiB) downloaded 57 time(s).