OSLO - Open Solving Library for ODEs

---

Functions list: RK547M(5), GearBDF(5)

RK547M(init, x1, x2, intvls, D) Implementation of Runge-Kutta algoritm with per-point accurancy control from Dormand and Prince article.
GearBDF(init, x1, x2, intvls, D) Implementation of Gear's BDF method with dynamically changed step size and order. Order changes between 1 and 3.

Arguments:

- init is either a vector of n real initial values, where n is the number of unknowns (or a single scalar initial value, in the case of a single ODE).
- x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODE(s) is evaluated. Initial values in init are the values of the ODE function(s) evaluated at x1.
- intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
- D is a vector function of the form D(x,y) specifying the right-hand side of the system

Options:

- AbsTol - absolute tolerance parameter, default value 10⁻⁷.
- RelTol - relative tolerance parameter, default value 10⁻⁴.
- MaxStep - maximal step value, default value x2-x1.

Links:

1. Open Solving Library for ODEs.
2. OSLO User Guide (pdf).

Open Solving Library for ODEs (OSLO) 1.0 User Guide.pdf (1 МиБ) скачан 85 раз(а).

oslo.integrate.sm (10 КиБ) скачан 115 раз(а).
oslo.kinetic1.sm (7 КиБ) скачан 96 раз(а).
oslo.kinetic2.sm (11 КиБ) скачан 103 раз(а).
oslo.kinetic3.sm (11 КиБ) скачан 93 раз(а).
oslo.test1.sm (15 КиБ) скачан 81 раз(а).
oslo.test2.sm (15 КиБ) скачан 95 раз(а).
oslo.Amplitude detector.sm (20 КиБ) скачан 95 раз(а).

oslo.integrate.pdf (88 КиБ) скачан 104 раз(а).
oslo.kinetic1.pdf (75 КиБ) скачан 95 раз(а).
oslo.kinetic2.pdf (91 КиБ) скачан 93 раз(а).
oslo.kinetic3.pdf (85 КиБ) скачан 91 раз(а).
oslo.test1.pdf (99 КиБ) скачан 85 раз(а).
oslo.test2.pdf (101 КиБ) скачан 95 раз(а).
oslo.Amplitude detector.pdf (149 КиБ) скачан 97 раз(а).

See also:

● [topic=726]Mathcad Toolbox[/topic]
● [topic=17088]Intel ODE Solver Library[/topic]
● [topic=1918]DotNumerics[/topic]
● [topic=13809]SADEL[/topic]
● [topic=1970]Matlab C++ Math Library[/topic]
● [topic=17067]lsoda[/topic]
● [topic=1997]GNU Scientific Library (GSL)[/topic]

Hello uni,

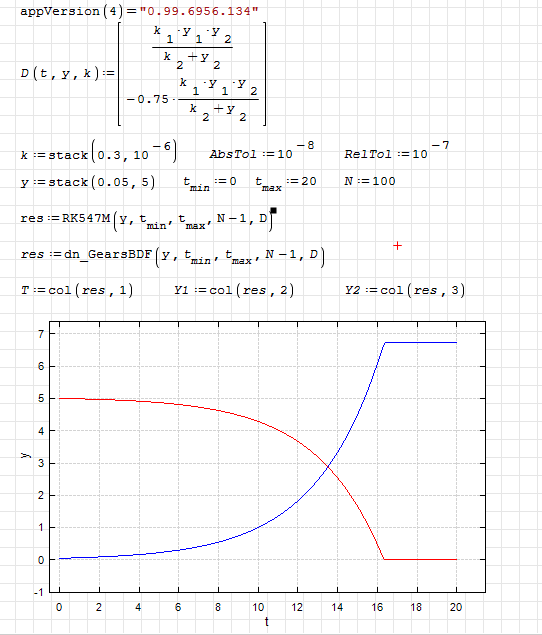
Thank you for some more ODE solvers. However, I could not resist to mention my favorite db_GearsBDF() which can escape the problem when y2 approaches zero. I mentioned this stiff example long time ago and you were using it often (kinetic2.sm example here). Unfortunately, it seams GearBDF() from this plugin can not overcome zero values and gets into the negative ones like most of the solvers.



Regards,
Radovan

Yes, weak solvers. There are some settings there, but I was not able to select them correctly for this task. Another strange problem with accuracy. Unlike other solvers, a smaller step is needed here. In general, there are questions to the developers (Microsoft Research and Moscow State University).
Not only dn_GearsBDF() can solve your task. Some other solvers have also achieved success. Still looking for the best. Not all solvers are still implemented, the test suite is also still small.

Wrote

... the test suite is also still small.

Hi Viacheslav. Maybe you're interested in check this matlab ode's:

http://people.sc.fsu.edu/~jburkardt%20/m_src/test_ode/test_ode.html .

At the end, there are also png images for the plots.

Best regards.

Alvaro.

And another one: TEST SET FOR IVP SOLVERS.

Wrote

And another one: TEST SET FOR IVP SOLVERS.

In this link it was mentioned about the book and packages made in R (Karline Soetaert et al). I was exposing my students to the R and some of their packages (deSolve, bvpSolve, rootSolve etc.) for few years now. I am really impressed by them. There are solvers for IVP, BVP, DAE, PDE etc. All my credits to the authors and their efforts. Surprisingly, there are quite a lot numerical packages in R which is considered to be mainly a statistical environment.

Regards,
Radovan

Wrote

In this link it was mentioned about the book and packages made in R (Karline Soetaert et al). I was exposing my students to the R and some of their packages (deSolve, bvpSolve, rootSolve etc.) for few years now. I am really impressed by them. There are solvers for IVP, BVP, DAE, PDE etc. All my credits to the authors and their efforts. Surprisingly, there are quite a lot numerical packages in R which is considered to be mainly a statistical environment.

Can't be more right Radovan: for using R, better be an R man
All those solvers fall in the category Lagrangian Methods quite evolved since CAS
Soon, there will be as many dedicated ODE solvers as they will be proved for
Physicals system to solve. dn_GearsBDF is a good companion for stiff systems,
and hyper fast [see comparison attached].


Jean

ODE HIRES.sm (57 КиБ) скачан 76 раз(а).

... Legendre_Radau updated wrt local definition

ODE HIRES.sm (67 КиБ) скачан 84 раз(а).

... thanks Radovan for the undocumented

ODE GearsBDF Undocumented.sm (9 КиБ) скачан 93 раз(а).

Wrote

... thanks Radovan for the undocumented

ODE GearsBDF Undocumented.sm (9 КиБ) скачан 93 раз(а).

You are welcome Jean, and thank you. There is another one by uni - lsoda.

Regards,
Radovan

Wrote

You are welcome Jean, and thank you. There is another one by uni - lsoda.

Thanks Radovan,
As it looks, the previous 8 ODE from Viacheslav are all Isoda.
Do you feel comfortable to code Smath ?
An all version(s) compatible will enhance the native tiny Smath.
Naturally, Smath does not solve the "Pulse". Does not recognize F(t).

Cheers ... Jean

Plugin updated.

Changes:

- added support for ODE systems in mathematical form;
- default value for MaxStep changed from h/2 to xmax-xmin;
- refactored.

Plugin updated.

Changes:

- solution restructured;
- converting the task for the ODE solver to the numerical form is now performed through the Mathcad Toolbox plugin (to avoid code duplication), so it must be installed;
- refactored.

Solvers that support mathematical notation now reuse code from the Mathcad Toolbox plugin. Now there is no need to recompile every such plugin.