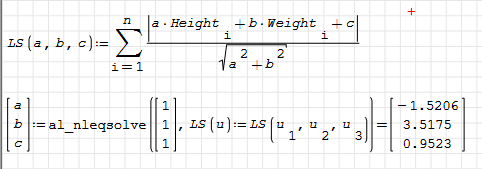1 страниц (11 вхождений)
SMath vs Mathcad - Сообщения
I can solve this problem in Mathcad - see pls the picture.
But cannot in SMath - see the SMath-file :-(
Help please

6-1-Mister-Class-a-b-c.sm (15,82 КиБ) скачан 1052 раз(а).
But cannot in SMath - see the SMath-file :-(
Help please

6-1-Mister-Class-a-b-c.sm (15,82 КиБ) скачан 1052 раз(а).
Thanks and sorry!
I do not see in your solution derivatives!
???
I do not see in your solution derivatives!
???
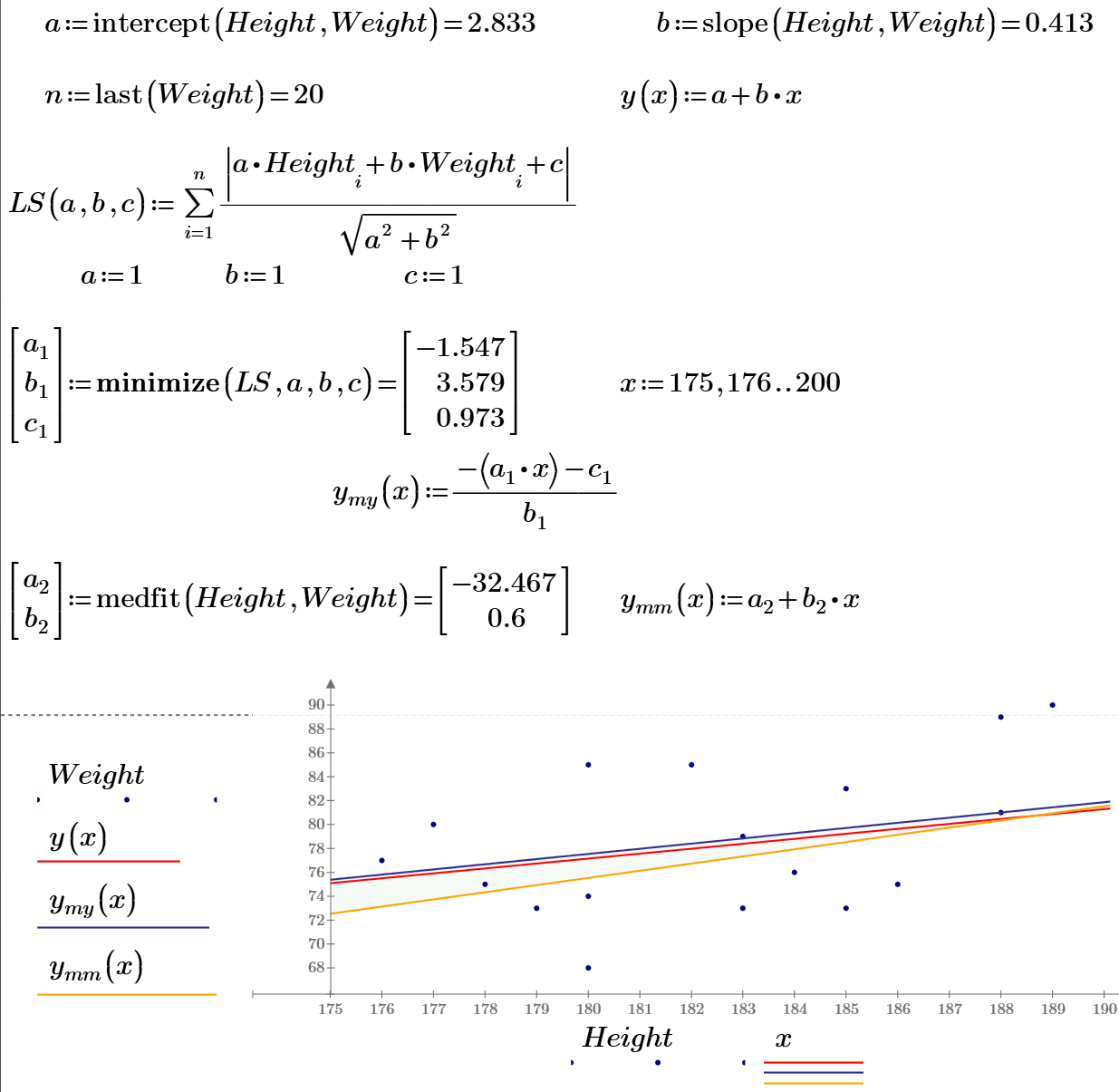
Here is a version with Maxima Fit(). Note that Fit() uses a least squares procedure, whereas Mathcad obviously directly minimizes the average linear distance between data points and model.
Ordinary linear regression with slope and intersect is a least squares fit for the vertical distance.
6-1-Mister-Class-a-b-c_kr.sm (35,92 КиБ) скачан 1044 раз(а).
![2024-08-06 13_32_52-SMath Solver - [6-1-Mister-Class-a-b-c_kr.sm_].png](/ru-RU/files/Download/gqc7pn/2024-08-06-13_32_52-SMath-Solver---[6-1-Mister-Class-a-b-c_kr.sm_].png)
Ordinary linear regression with slope and intersect is a least squares fit for the vertical distance.
6-1-Mister-Class-a-b-c_kr.sm (35,92 КиБ) скачан 1044 раз(а).
![2024-08-06 13_32_52-SMath Solver - [6-1-Mister-Class-a-b-c_kr.sm_].png](/ru-RU/files/Download/gqc7pn/2024-08-06-13_32_52-SMath-Solver---[6-1-Mister-Class-a-b-c_kr.sm_].png)
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
1 пользователям понравился этот пост
Valery Ochkov 06.08.2024 18:53:00
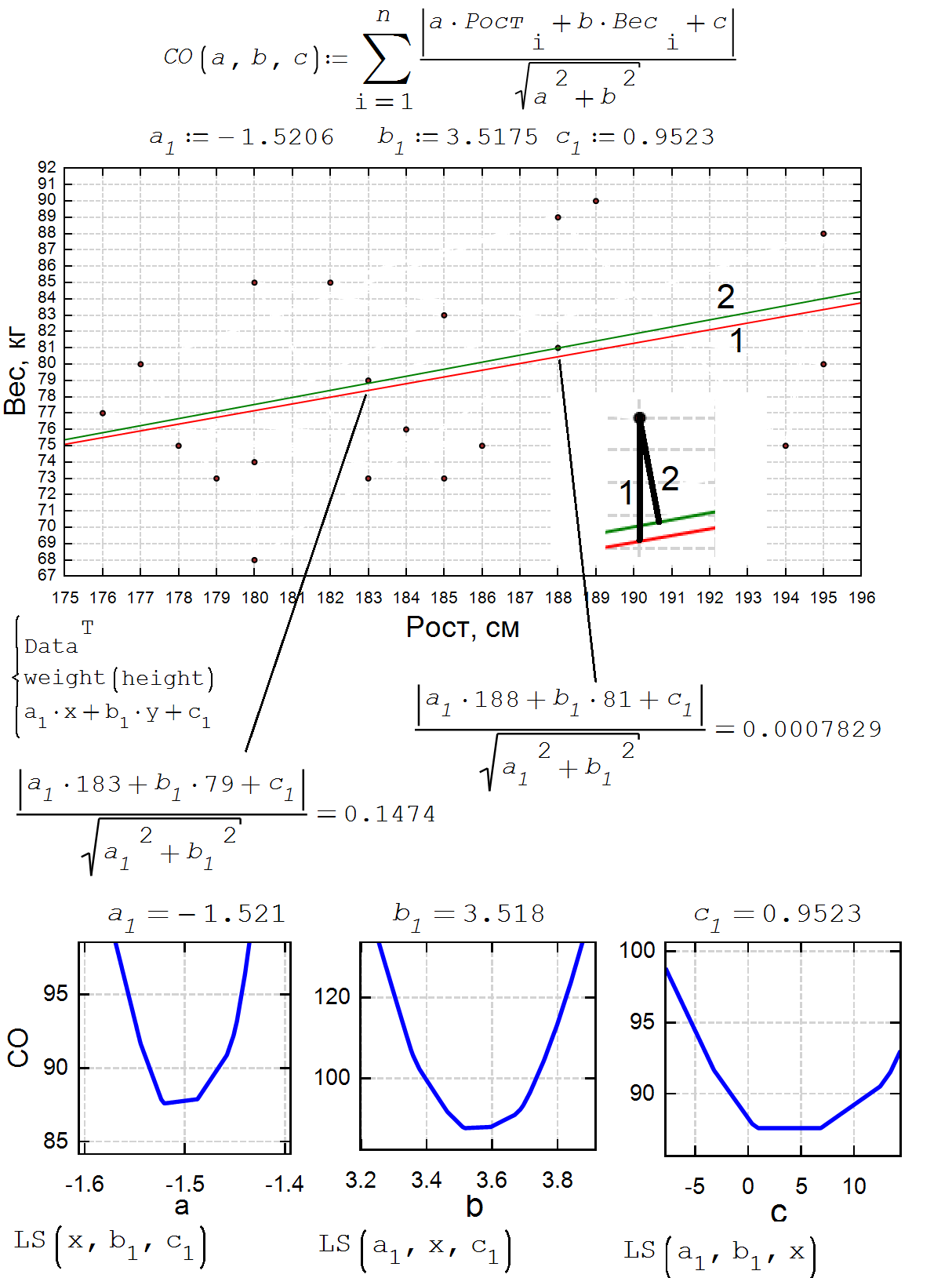
Interesting paper. Yet the authors keep one question out of scope: In case of orthogonal distance minimizing (be it linear or quadratic), rescaling of the data matter. (other than with ordinary linear regression). This means that you get different results if you provide your data not in cm but in mm.
Perhaps the data should be scaled such that the uncertainty (measurement error) is of similar numeric value for x and y.
Perhaps the data should be scaled such that the uncertainty (measurement error) is of similar numeric value for x and y.
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
Wrote
The perpendicular distance is only geometrically perpendicular in the graph if the axes tick ratio is 1 (as I tried to set in my earlier post) unless you introduce an anisotropic metric for the distance (or standardize the quantities).
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
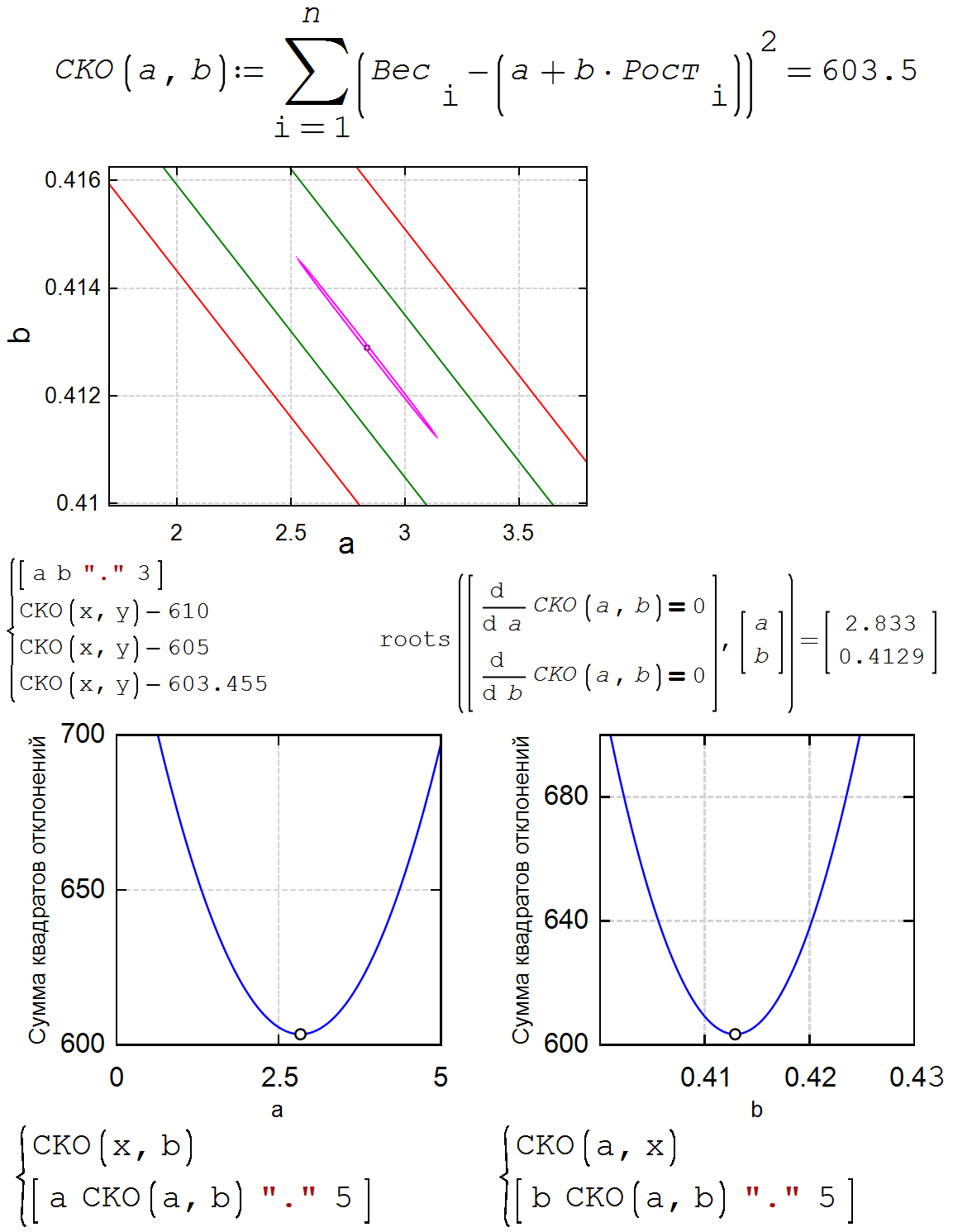
Hi. Chosen different guess values, we can reproduce the maxima result. Also, notice that meanwhile the Maxima MSE function decreases, the "classical" one increases. I'm not sure how to call Maxima MSE for implicit functions.
mse.sm (25,22 КиБ) скачан 1043 раз(а).
Best regards
Alvaro
mse.sm (25,22 КиБ) скачан 1043 раз(а).
Best regards
Alvaro
1 страниц (11 вхождений)
- Новые сообщения
- Нет новых сообщений