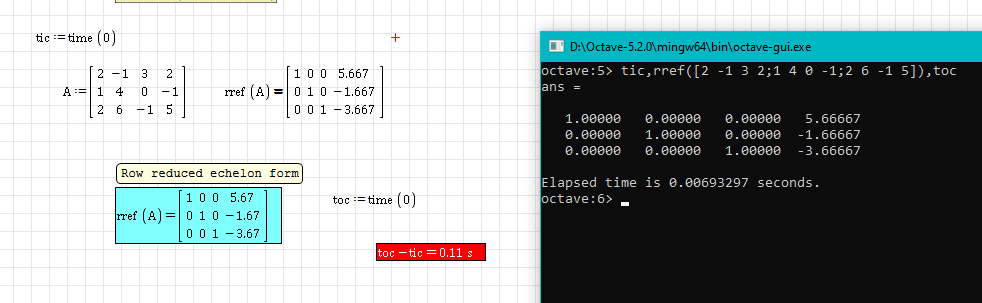
Row Reduced Echelon Form - RREF - Native SMath Studio, no plugins - Messages
#1 Posted: 5/20/2020 7:30:31 PM
Hello,
I am sharing with you these functions I have created today:
1. randi() (as in Octave)
2. echelon() echelon form of a given matrix
3. rref() row reduced echelon form of a given matrix
I know that this last function is not available in Maxima, therefore, with Maxima plugin we can use echelon() but not rref().
It would be great if you can test the function and improve the calculation time.
Regards,
Alvaro
SMath Studio:
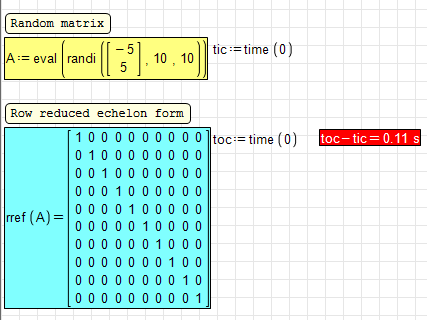
GNU Octave:

File:
RREF.sm (22.45 KiB) downloaded 798 time(s).
I am sharing with you these functions I have created today:
1. randi() (as in Octave)
2. echelon() echelon form of a given matrix
3. rref() row reduced echelon form of a given matrix
I know that this last function is not available in Maxima, therefore, with Maxima plugin we can use echelon() but not rref().
It would be great if you can test the function and improve the calculation time.
Regards,
Alvaro
SMath Studio:

GNU Octave:

File:
RREF.sm (22.45 KiB) downloaded 798 time(s).
#2 Posted: 5/20/2020 10:07:12 PM
WroteIt would be great if you could test the function ...
It fails an ordinary m*n matrix.
RREF fails.sm (25.02 KiB) downloaded 691 time(s).
#4 Posted: 5/21/2020 7:47:26 AM
Please, attach the Smath document working code.
The bug may be wrt your SS 7030 my SS 6179 ?
The bug may be wrt your SS 7030 my SS 6179 ?
#5 Posted: 5/22/2020 6:02:11 AM
Hola Alvaro.
Nice routines. Just some few notes:
- You forget to divide by the next nonzero column element when the diagonal element M[k,k] = 0. In other words: you get different results than other software for singular matrices.
- The use of i as counter make the routine useless for complexes.
- Instead of row(M,k)[j] (in SMath string is el(row(M,k),j) ) you can use M[k,j] (this is el(M,k,j) in SMath).
- eval make the routine faster, specially for the stack function. But it introduce more roundoff errors. You can see that in an example where rref make zero any element outside the left identity matrix.
- Also, eval make unreadable the symbolic evaluation, because some functions are not evaluated for symbolics, like stack.
- With some effort, you can write the routine using range variables as matrices and vectors subscripts, in a similar (but not identical) way in matlab.
Best regards.
Alvaro.
Nice routines. Just some few notes:
- You forget to divide by the next nonzero column element when the diagonal element M[k,k] = 0. In other words: you get different results than other software for singular matrices.
- The use of i as counter make the routine useless for complexes.
- Instead of row(M,k)[j] (in SMath string is el(row(M,k),j) ) you can use M[k,j] (this is el(M,k,j) in SMath).
- eval make the routine faster, specially for the stack function. But it introduce more roundoff errors. You can see that in an example where rref make zero any element outside the left identity matrix.
- Also, eval make unreadable the symbolic evaluation, because some functions are not evaluated for symbolics, like stack.
- With some effort, you can write the routine using range variables as matrices and vectors subscripts, in a similar (but not identical) way in matlab.
Best regards.
Alvaro.
#6 Posted: 5/22/2020 7:45:57 AM
#7 Posted: 5/22/2020 9:01:25 AM
The brute force example reproduces both: Mathcad 11/Maple Smath.
Considering an m x n real matrix. Your finished code will be
appreciated so to enrich native Smath.
As it looks, rref is essentially built around 3 pieces of sub codes.
Cheers ... Jean
Maths rref.sm (31.01 KiB) downloaded 701 time(s).
Considering an m x n real matrix. Your finished code will be
appreciated so to enrich native Smath.
As it looks, rref is essentially built around 3 pieces of sub codes.
Cheers ... Jean
Maths rref.sm (31.01 KiB) downloaded 701 time(s).
#8 Posted: 5/22/2020 9:28:11 AM
Thank you Jean. Yes, esentially I need "echelon" function to make "rref" (although echelon is already built in Maple or Maxima plugin).
But now I see where my function ech() is failing, as Alvaro indicates, the roundoff errors have been trapped...
(I manually regulate the "gen" range to see the echelon process)
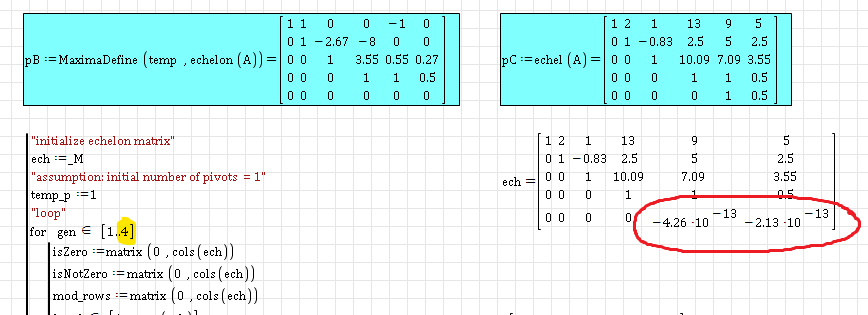
But now I see where my function ech() is failing, as Alvaro indicates, the roundoff errors have been trapped...
(I manually regulate the "gen" range to see the echelon process)

1 users liked this post
frapuano 5/22/2020 2:58:00 PM
#9 Posted: 5/22/2020 5:19:14 PM
The regular way to use Maxima functions is via the Maxima() function. In your case MaximaDefine() defines a variable temp in the curent maxima session. If you just want to display or use the value in the current SMath sheet, then Maxima() is sufficient and thanks to Davide's custom glyph looks better.
![2020-05-22 22_02_31-SMath Studio - [RREF.sm_].png](/en-US/files/Download/TcCohq/2020-05-22-22_02_31-SMath-Studio---[RREF.sm_].png)
![2020-05-22 22_02_31-SMath Studio - [RREF.sm_].png](/en-US/files/Download/TcCohq/2020-05-22-22_02_31-SMath-Studio---[RREF.sm_].png)
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#10 Posted: 5/22/2020 5:47:24 PM
Wow, thanks Martin! I didn't know about that, I was wondering about the purpose of the temp variable.. and nice glyph! I recently discovered Maxima and started to learn using the cmd (with your book and the extensive Maxima documentation). How powerful CAS it is.
#11 Posted: 5/22/2020 6:44:45 PM
There is a lot to find about Maxima in the interactive handbook. It is sort of out of maintenances. Some examples would need adjustment to recent changes in how SMath evaluates expressions but you still get the idea.
In the interactive handbook, goto Plugins> Maxima. This leads you to an overview with links to all related functions. The interactive handbook is bilingual german/english throughout. You see the version based on your gui language setting in SMath Studio.
In the interactive handbook, goto Plugins> Maxima. This leads you to an overview with links to all related functions. The interactive handbook is bilingual german/english throughout. You see the version based on your gui language setting in SMath Studio.
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#12 Posted: 5/23/2020 12:41:23 AM
Thank you Martin, I didn't know about that interactive book, recently read quickly and found very useful the Maxima tester, tomorrow I will take a deeper look, as I am preparing some introductory class to SMath Studio for students learning linear algebra (it's on Sunday)..they already use Matlab, but I think that the "linearalgebra" collection of functions is very useful.
#13 Posted: 5/23/2020 1:10:29 AM
By the way, I have a new version of the rref() function, with pros/cons.
I prepared "rounds" to test and compare the rref() from Maple, and the created rref(). Rounds -5 to 0 are easy ones, rounds 1 to 9 are normal matrices, and round 10...the final and most exigent, creates a matrix with random size and random numbers. Now I finally can tell that all rounds resulted in rref_AGR=rref_MAPLE...I have tested round 10 recalculating randomness (F9), and got equivalence 50 times in a row (matrix with zeros and ones, with size up to 25x25...fast calculation).
There is an interesting factor that rref_AGR is computed a few milliseconds faster than rref_MAPLE in most cases (in small matrices)
My big problem is calculation time, as I needed to delete eval() to generate exact zeros.
This problem appears with a matrix greater than 10x10 and numbers within a range with absolute values above 9 or 10.
I would really appreciate that you can test the function, especially in round 10.
Regards,
Alvaro
RREF.sm (161.37 KiB) downloaded 699 time(s).
.png)
I prepared "rounds" to test and compare the rref() from Maple, and the created rref(). Rounds -5 to 0 are easy ones, rounds 1 to 9 are normal matrices, and round 10...the final and most exigent, creates a matrix with random size and random numbers. Now I finally can tell that all rounds resulted in rref_AGR=rref_MAPLE...I have tested round 10 recalculating randomness (F9), and got equivalence 50 times in a row (matrix with zeros and ones, with size up to 25x25...fast calculation).
There is an interesting factor that rref_AGR is computed a few milliseconds faster than rref_MAPLE in most cases (in small matrices)
My big problem is calculation time, as I needed to delete eval() to generate exact zeros.
This problem appears with a matrix greater than 10x10 and numbers within a range with absolute values above 9 or 10.
I would really appreciate that you can test the function, especially in round 10.
Regards,
Alvaro
RREF.sm (161.37 KiB) downloaded 699 time(s).
.png)
#14 Posted: 5/23/2020 2:32:37 AM
Wrote
My big problem is calculation time, as I needed to delete eval() to generate exact zeros.
Hi. Actually, even it's true that eval introduce some roundoff errors, SMath in numerics it's capable by itself to introduce a lot of others. Try with coefficients like sqrt(2) or any transcendental function.
I try to avoid eval for symbolics, not just for those roundoff errors.
A way where you can use eval and minimize the number of near zero values is defining your own SameQ( a,b ) instead to try to eval only a=b, with something like abs( a-b )<10e-12. In the attached I use this way but for compare symbolic values with zero, and assume that if isn't the string "0", the maybe it is not zero.
Notice that because SameQ is defined after the GaussElim function, you can change it, and reuse the same code.
This is my simplified routine for the echelon form, but consistent with the old linalg maple package, which is implemented as gausselim. Even that, I don't get the same result for some symbolics situations, where the maple evalb maybe works different from my SameQ function.
GaussElim.sm (25.71 KiB) downloaded 665 time(s).
GaussElim.pdf (91.35 KiB) downloaded 399 time(s).
Best regards.
Alvaro.
1 users liked this post
frapuano 5/23/2020 5:08:00 AM
#15 Posted: 5/23/2020 3:00:11 AM
Wrote
There is an interesting factor that rref_AGR is computed a few milliseconds faster than rref_MAPLE in most cases (in small matrices)
To evaluate each expression a separate call to the interpreter is launched. I can speed up the function if I'll work with only one instance of the interpreter. Therefore, time is spent not only on calculations, but also on auxiliary actions associated with file I / O and the launch of the process.
Russia ☭ forever, Viacheslav N. Mezentsev
#16 Posted: 5/23/2020 8:48:00 AM
QuoteThis is my simplified routine for the echelon form
Thanks Alvaro, really, your routine reveals to me what I was misunderstanding when you told me to use variable ranges...it is practically working like the Octave M(:,1) or M(2,: ) to call an entire first column or second row of a matrix. I will try to shorten my routine now. Thanks again!
QuoteTherefore, time is spent not only on calculations, but also on auxiliary actions associated with file I / O and the launch of the process.
Thanks uni! It was a false feeling that my routine is faster..haha, it only happens with very small matrices. Maple(rref() does its job when it comes to larger matrices. Personally, I don't think it is necessary to improve calculation time, that time not spent on calculations is about 80 ms..practically nothing. Wonderful plugin, and many thanks to you!
#17 Posted: 5/23/2020 6:04:16 PM
Again thank you very much Alvaro! I followed your suggestion, and learned about improving calculation in SMath Studio. I changed my code to your style, with variable ranges, and it is really awesome that I did not need the eval() function, neither the roundtozero() function to interpret as zero, to stay competitive with Maple.
As you can see, in my functions I use the stack() function only once, and deleted the other stack(), augment(), matrix() functions that I think were slowing symbolic calculation. So I am staying symbolic!
These are the results for 10 evaluations in round 10 with Maple. Competitive!!

RREF.sm (256.52 KiB) downloaded 723 time(s).
Ok last one, for fun.. 4.33 min vs 6.30 min

As you can see, in my functions I use the stack() function only once, and deleted the other stack(), augment(), matrix() functions that I think were slowing symbolic calculation. So I am staying symbolic!
These are the results for 10 evaluations in round 10 with Maple. Competitive!!

RREF.sm (256.52 KiB) downloaded 723 time(s).
Ok last one, for fun.. 4.33 min vs 6.30 min

#18 Posted: 5/23/2020 7:26:50 PM
#19 Posted: 5/23/2020 8:35:17 PM
Hi. My codes usually are very slow, but try to write them simplest as possible. As advanced users says here in the forum, speed test depends of the machine and the operating system, so usually are not comparable between different users.
Here my numeric-symbolic routine for rref, and the candidate to be a numeric one.
GaussElim.sm (188.01 KiB) downloaded 722 time(s).
GaussElim.pdf (326.74 KiB) downloaded 424 time(s).
Best regards.
Alvaro.
PD: I'm not sure if it's a good idea to compare maple with smath, because maple have variable precision arithmetic, vpa, which is very good for mix symbolic and numeric results. I don't know if in version 6, maple use some lapac routine or what, when detect non-exact numbers. Usually in maple, you can set any number with a period, and then maple take it as floating point number, and call specialized numeric routines.
Here my numeric-symbolic routine for rref, and the candidate to be a numeric one.
GaussElim.sm (188.01 KiB) downloaded 722 time(s).
GaussElim.pdf (326.74 KiB) downloaded 424 time(s).
Best regards.
Alvaro.
PD: I'm not sure if it's a good idea to compare maple with smath, because maple have variable precision arithmetic, vpa, which is very good for mix symbolic and numeric results. I don't know if in version 6, maple use some lapac routine or what, when detect non-exact numbers. Usually in maple, you can set any number with a period, and then maple take it as floating point number, and call specialized numeric routines.
#20 Posted: 5/23/2020 9:27:35 PM
- New Posts
- No New Posts