Wrote

To be honest, in order to replace Mathcad (Prime) and use SMath completely in my teaching, I need only few more things (like nonlinear curve fitting) but time is passing and I am still waiting o_o . I have enough time for that, but would like to be ASAP.

It is easily to find out that these few things are needed for majority of the engineering math and modeling problems. SMath's visual capabilities are very attractive for engineering applications.

- system of linear equations (SMath - should be improved)
- system of nonlinear equations (SMath - roots(), not good enough - plugin made by w3b5urf3r)
- system of first order ODE (SMath - plugin made by uni, improving appreciated)
- interpolation (SMath - included, should be improved)
- differentiation, integration (SMath - should be improved)
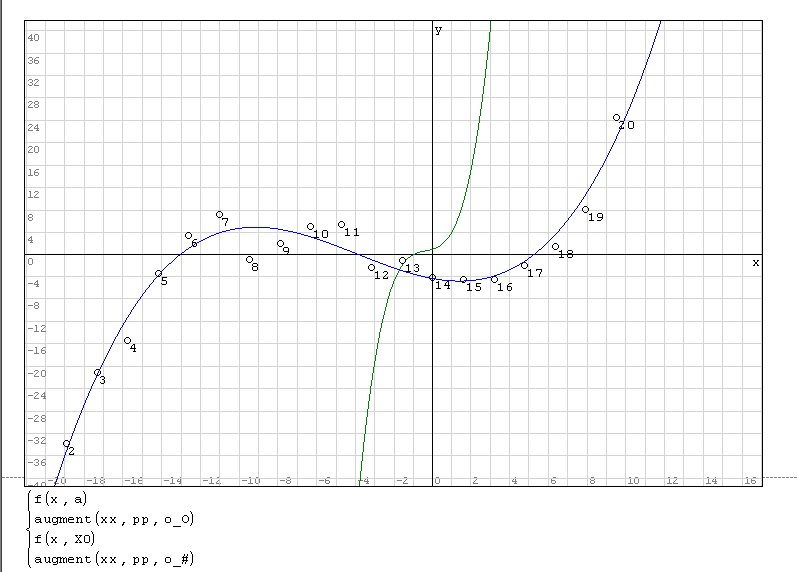
- linear and nonlinear curve fitting (SMath - not included, neither plugins made)
- 2D and 3D plotting (SMath - should be improved)
- units (SMath - quite good enough)

Hi omorr, this is a useful reference for Andrey and plugin developers.
Could you elaborate more each section ? by specifying which features should be added/improved/corrected.

Hello kilele,

I hope you would not mind, but I suggest you to search the Forum and to see some of my posts. As you could see, there are almost one thousand of them (I sometimes hesitate to post because of being annoying with so many of them). Whatever I would write here, would be repeating the things I already mentioned. By the way, you also mentioned and posted many links to numerical algorithms and methods . I respect any developer who is willing to put all those methods and keep them "alive" in SMath, but eventually it will take quite a long time.

Actually, the priorities in SMath development are up to the Andrey's decisions and he knows the best about it.

Regards,
Radovan

I updated the plugin now works more stable.

---

Draghilev's method. NLS. Example 2.smz (6 KiB) downloaded 109 time(s).

You are right uni, thank you

Now, every F9 produces result for your test problem.

Regards,
Radovan

20 points (~24 sec). I made some little changes in Draghilev() function.

---

Draghilev's method. NLS. Example 2.smz (6 KiB) downloaded 102 time(s).

Hello uni,

It is quite interesting that you've made it working with 20 points .
By the way, I've added the sum of squares - just to check how this sum reduces its value.

Regards,
Radovan

---

Yes, but initial value for a is X0 := stack(1, 1, 1, 1)

Wrote

Yes, but initial value for a is X0 := stack(1, 1, 1, 1)

Sorry, uni, my mistake . Graph distracted me

In this example - this is really amazing

If this could work for a bit more complicates functions - it would be really great .

Regards,
Radovan

---

Wrote

By the way, I bumped many times into the derivative, gradient, Jacobian problem in SMath and almost always had to give it up. I even asked Andrey few times to introduce numerical differentiation in spite of the well known fact that numerical differentiation is prone to numerical errors. Calculating even derivatives (Jacobian is another nightmare) analytically is sometimes almost impossible and there is no other way than using some kind of numerical approximation. Therefore, when Jacobian is involved in some calculation - I always find myself unconfortable

Please look at these matlab algorithms:

See pdfpage 112/docpage 90 of this document for a jacobian approximation by finite difference
http://www.dsic.upv.es/docs/bib-dig/tesis/etd-10272003-001792/TesisEnriqueArias.pdf

Adaptive Robust Numerical Differentiation (matlab code)
http://www.mathworks.com/matlabcentral/fileexchange/13490-adaptive-robust-numerical-differentiation

Quote

Thank you for considering this . If you include the sum of squares to your example above, then it is equivalent as finding the roots of this three equations

[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a1)),i,1,n)≡0[/MATH]

[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a2)),i,1,n)≡0[/MATH]

[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a3)),i,1,n)≡0[/MATH]

It is a well known and maybe redundant to say, sorry - the first derivatives over three unknowns (a1,a2,a3) should be zero

Now I knew where it came from. I also fixed a bug with double index ii. I've used it twice.

---

Draghilev's method. NLS. Example 2.1.smz (6 KiB) downloaded 100 time(s).

Hello uni,

It seems very promising

As it is basically a linear regression over parameters (polynomial equation) I just added the result of it - just for checking. The results are very close to each other. It is interesting that the method is working on this problem very well
The determinant [MATH=eng]det((transpose(XX)*XX))=2.40082615642816*10^16[/MATH]is rather far from zero - well conditioned system. I suppose that would be very interesting to see what will happen when this determinant is quite close to zero - ill conditioned system. I suppose that the results must be quite different.

Regards,
Radovan

---

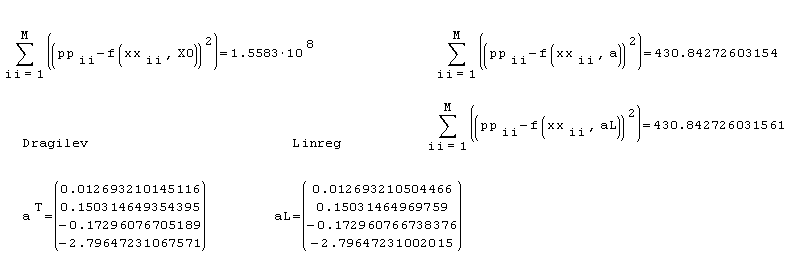
Quote

I suppose that would be very interesting to see what will happen when this determinant is quite close to zero - ill conditioned system. I suppose that the results must be quite different.

Yes, it would be interesting. I'll try to find an example. To improve accuracy, we can increase the parameter N. As for the more complex functions, I'm working on it.

Hello kilele,

Wrote

Wrote

By the way, I bumped many times into the derivative, gradient, Jacobian problem in SMath and almost always had to give it up. I even asked Andrey few times to introduce numerical differentiation in spite of the well known fact that numerical differentiation is prone to numerical errors. Calculating even derivatives (Jacobian is another nightmare) analytically is sometimes almost impossible and there is no other way than using some kind of numerical approximation. Therefore, when Jacobian is involved in some calculation - I always find myself unconfortable

Please look at these matlab algorithms:

See pdfpage 112/docpage 90 of this document for a jacobian approximation by finite difference
http://www.dsic.upv.es/docs/bib-dig/tesis/etd-10272003-001792/TesisEnriqueArias.pdf

Adaptive Robust Numerical Differentiation (matlab code)
http://www.mathworks.com/matlabcentral/fileexchange/13490-adaptive-robust-numerical-differentiation

Thank you for the links. Actually, that is the point. At the moment, many plugins which rely on symbolic derivative, gradient, Jacobian, Hessian have great chance to fail sometimes due to the SMath symbolic restrictions and features or simply due to a complicated expressions obtained. There were many situations when you can actually have the numerical values of a vector valued function, but you can not have the derivatives of its elements (therefore, can not calculate Jacobian, Hessian etd.) and every method who use this will also fail (take a look for instance at the efforts of w3b5urf3r an the Nonlinear-solvers plugin). We can actually make Jacobian function ourselves (like the one very simple and hardly useful as in the attached example), but I think that is not the point. Numerical derivation methods are quite prone to errors and I would very like that someone make a plugin (based on some more sophisticated algorithms) like the one mentioned in your second link.

Regards,
Radovan

---

Jacnum.sm (16 KiB) downloaded 92 time(s).

Radovan, it's really hard to get a solution using the Draghilev method. I do not know how to do it yet.

The solution here is: [28.4502559095434933, -2720.12633981294994, -7.01208324395984839]. Maybe later I'll be able to get it.

---

Do not worry about it uni ,

I think it is good enough that you solved many other examples including this particular problem .

Regards,
Radovan

Experience shows that the Draghilev's method is most effective when searching for an infinite set of solutions, when f1 ... fm, x1 ... xn and n>m ...

Wrote

... not worry... uni ,

Be happy.

Example 2. Finding roots: System 1 (Mathcad 15)

[MATH]sys(x^2-y*x+y^2-1=0;sin(5*x^2)+sin(4*y^2)=0;2;1)[/MATH]

---

Draghilev's method. Finding roots. System 1. MC15_M010_20110622.zip (283 KiB) downloaded 99 time(s).

Example 5. Finding roots: System 4.


[MATH]sys(x^2+y^2-8=0;sin(x*y)*sin(exp(x*y))=0;2;1)[/MATH]

I made minor changes to simplify the calculations. Function has become more clear.

Calculation time: ~1.5 min
Roots: 80

---

x1^3+x2^3-0.1e-1*sin(1.0001*x1+x2)=0;
One equation with two unknowns or implicitly given function. In the figure we can see the points at which violated the conditions of existence of an implicit function.

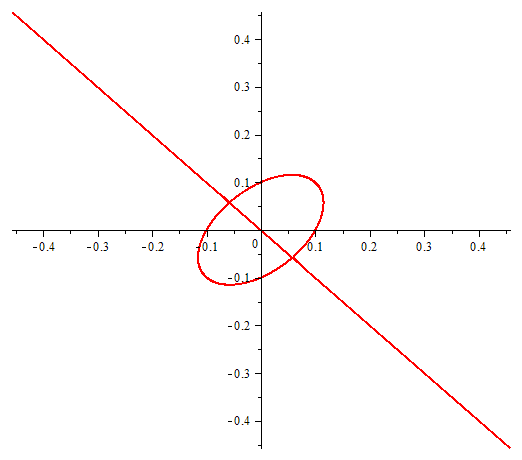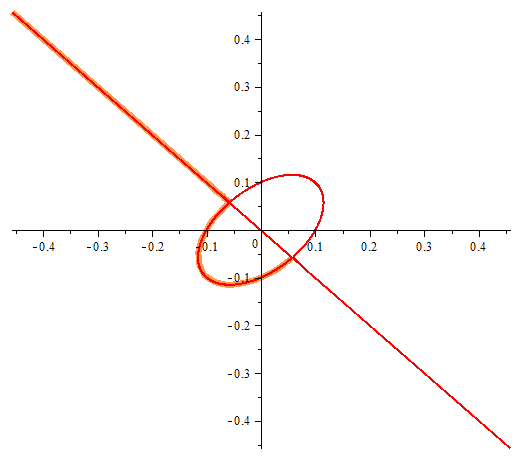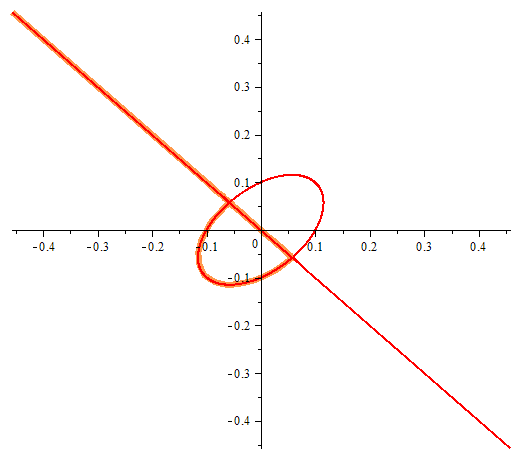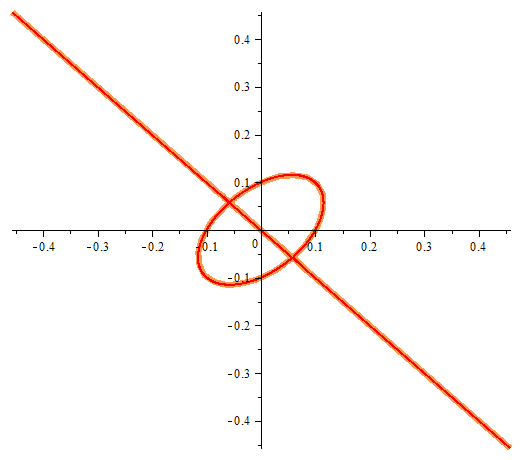
Draghilev's method.
x1 and x2 are solutions of this equation and are functions of the arc length, which allows a clear move along places where there are no implicit function in the classically accepted terms …

Examples updated.

Draghilev's method. Finding roots. System 0.sm (348 KiB) downloaded 69 time(s).
Draghilev's method. Finding roots. System 0.pdf (316 KiB) downloaded 77 time(s).

Draghilev's method. Finding roots. System 1.sm (324 KiB) downloaded 72 time(s).
Draghilev's method. Finding roots. System 1.pdf (329 KiB) downloaded 66 time(s).

Draghilev's method. Finding roots. System 2.sm (29 KiB) downloaded 69 time(s).
Draghilev's method. Finding roots. System 2.pdf (91 KiB) downloaded 75 time(s).

Draghilev's method. Finding roots. System 3.sm (306 KiB) downloaded 65 time(s).
Draghilev's method. Finding roots. System 3.pdf (306 KiB) downloaded 63 time(s).

Draghilev's method. Finding roots. System 4.sm (69 KiB) downloaded 66 time(s).
Draghilev's method. Finding roots. System 4.pdf (160 KiB) downloaded 61 time(s).