Draghilev's method - Solving systems of nonlinear equations. - Messages
#1 Posted: 10/2/2012 7:16:14 AM
It seems that now there is all I needed to demonstrate the method. I will try to show step by step how to use the solver. As for the theory, Alexey will help me.
Example 1. Finding extremes: Himmelblau's function:
[MATH]f(x;y) : (x^2+y-11)^2+(x+y^2-7)^2[/MATH]
[MATH]sys(4*x^3+4*x*y-42*x+2*y^2-14=0;2*x^2+4*x*y+4*y^3-26*y-22=0;2;1)[/MATH]
P. S. Buchberger's algorithm can solve systems like that much easer.
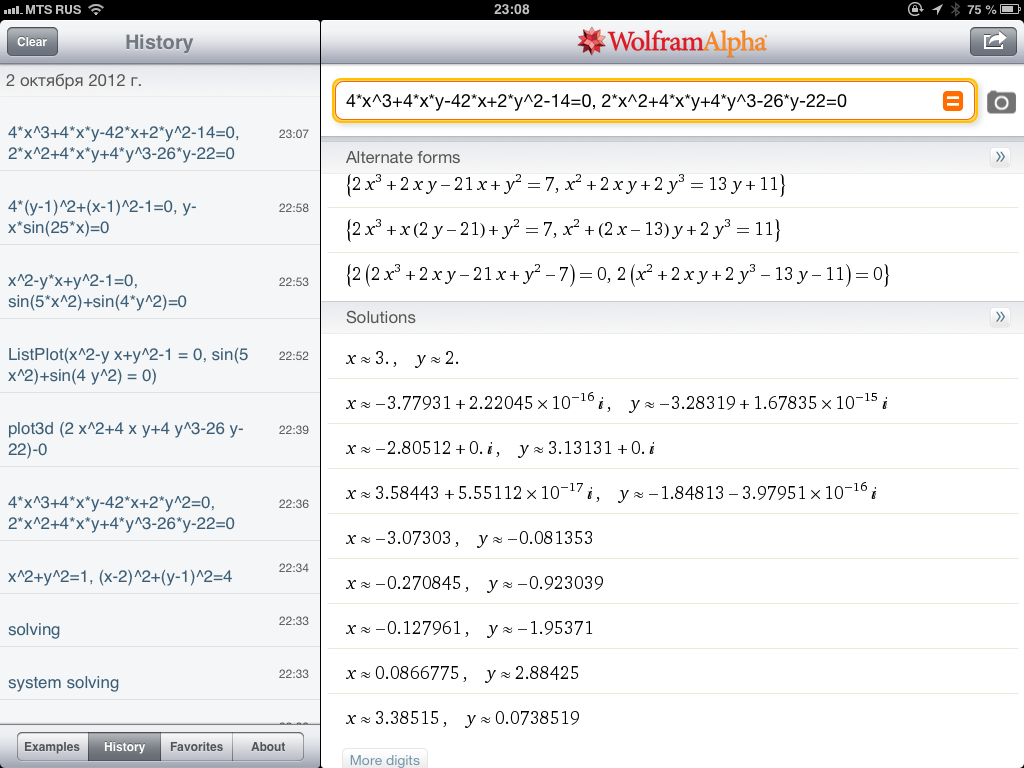
Example 1. Finding extremes: Himmelblau's function:
[MATH]f(x;y) : (x^2+y-11)^2+(x+y^2-7)^2[/MATH]
[MATH]sys(4*x^3+4*x*y-42*x+2*y^2-14=0;2*x^2+4*x*y+4*y^3-26*y-22=0;2;1)[/MATH]
P. S. Buchberger's algorithm can solve systems like that much easer.
Russia ☭ forever, Viacheslav N. Mezentsev
2 users liked this post
#4 Posted: 10/3/2012 12:51:52 AM
Example 4. Finding roots: System 3.
[MATH]sys(3*x-cos(y*z)-1/2=0;x^2-81*(y+0.1)^2+sin(z)+1.06=0;20*z+e^{-x*y}+1/3*(-3+10*π)=0;3;1)[/MATH]
P.S. The picture was obtained in MC11 and visualized in MC15 (my own implicitplot3d() function).
Draghilev's method. Finding roots. System 3.smz (351 KiB) downloaded 154 time(s).
[MATH]sys(3*x-cos(y*z)-1/2=0;x^2-81*(y+0.1)^2+sin(z)+1.06=0;20*z+e^{-x*y}+1/3*(-3+10*π)=0;3;1)[/MATH]
P.S. The picture was obtained in MC11 and visualized in MC15 (my own implicitplot3d() function).
Draghilev's method. Finding roots. System 3.smz (351 KiB) downloaded 154 time(s).
Russia ☭ forever, Viacheslav N. Mezentsev
#5 Posted: 10/3/2012 11:26:54 PM
Example 4. Finding roots: System 3 version 0.3 (thanks Alvaro for the optimization of the search function)
Draghilev's method as a single function (dimension >= 2).
Draghilev's method. Finding roots. System 3 version 0.3.smz (336 KiB) downloaded 148 time(s).
Draghilev's method as a single function (dimension >= 2).
Draghilev's method. Finding roots. System 3 version 0.3.smz (336 KiB) downloaded 148 time(s).
Russia ☭ forever, Viacheslav N. Mezentsev
#6 Posted: 10/4/2012 12:20:41 AM
Example 2. Finding roots: System 1 version 0.2 (in one sheet).
Draghilev's method. Finding roots. System 1 version 0.2.smz (357 KiB) downloaded 132 time(s).
Draghilev's method. Finding roots. System 1 version 0.2.smz (357 KiB) downloaded 132 time(s).
Russia ☭ forever, Viacheslav N. Mezentsev
#7 Posted: 10/4/2012 1:18:16 AM
As far as I can see there are no questions. As I said, everything is quite simple - we follow along the curve of n+1 space. Next, I will tell how to choose a start point, direction, and about the restrictions that follow from the method. I hope that the examples will be added.
Draghilev's method. Finding extremes. Himmelblau function version 0.2.smz (334 KiB) downloaded 131 time(s).
Draghilev's method. Finding extremes. Himmelblau function version 0.2.smz (334 KiB) downloaded 131 time(s).
Russia ☭ forever, Viacheslav N. Mezentsev
#8 Posted: 10/4/2012 4:24:17 AM
Hello uni,
I tried to use your files explaining how to find extremes of the Himmelblau's function and to apply this to NLS (nonlinear least squares) problem to my example file NLminimization, but without success. As I expected, The Jacobian was the first problem. I struggled many times with obtaining Jacobian of the object function S( b ) , or f( x,y,z ) in this and similar examples, and SMath could not find the derivatives most of the time. For some other cases it was sometimes rather time consuming. It seems to be complex for the SMath engine to apply any Jacobian based minimization to this kind of problem. You could see in the attached file where I stopped.
I do not know if there is any sense to use Jacobian based minimization procedure to these kind of problems in SMath. I would appreciate any comment from you regarding this.
Regards,
Radovan
Draghilev's%20method-NLS.sm (202 KiB) downloaded 130 time(s).
I tried to use your files explaining how to find extremes of the Himmelblau's function and to apply this to NLS (nonlinear least squares) problem to my example file NLminimization, but without success. As I expected, The Jacobian was the first problem. I struggled many times with obtaining Jacobian of the object function S( b ) , or f( x,y,z ) in this and similar examples, and SMath could not find the derivatives most of the time. For some other cases it was sometimes rather time consuming. It seems to be complex for the SMath engine to apply any Jacobian based minimization to this kind of problem. You could see in the attached file where I stopped.
I do not know if there is any sense to use Jacobian based minimization procedure to these kind of problems in SMath. I would appreciate any comment from you regarding this.
Regards,
Radovan
Draghilev's%20method-NLS.sm (202 KiB) downloaded 130 time(s).
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#9 Posted: 10/4/2012 6:47:37 AM
#10 Posted: 10/4/2012 7:36:12 AM
But it is possible.
P.S. This is not a correct example too, the determinant is zero. The sum of squares must be on all points.
Draghilev's method. Approximation. Simple example.smz (5 KiB) downloaded 128 time(s).
P.S. This is not a correct example too, the determinant is zero. The sum of squares must be on all points.
Draghilev's method. Approximation. Simple example.smz (5 KiB) downloaded 128 time(s).
Russia ☭ forever, Viacheslav N. Mezentsev
#11 Posted: 10/4/2012 9:05:42 AM
Hello uni,
Thank you for considering this . If you include the sum of squares to your example above, then it is equivalent as finding the roots of this three equations
. If you include the sum of squares to your example above, then it is equivalent as finding the roots of this three equations
[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a1)),i,1,n)≡0[/MATH]
[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a2)),i,1,n)≡0[/MATH]
[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a3)),i,1,n)≡0[/MATH]
It is a well known and maybe redundant to say, sorry - the first derivatives over three unknowns (a1,a2,a3) should be zero. The Jacobian of these three equations should not be zero (say, giving all xx different).
The problem is in derivatives, Jacobi matrix etc. (includes summation and quite large expressions). Whenever I tried to solve this root finding problem in SMath, finding derivatives, Jacobian etc. causes the main problem.
Anyway, could you please try to solve with this method the three above equations using your example function, but with more than three points.
Regards,
Radovan
P.S. I just saw that you added smz file as well. I might try myself ass well - but have doubts that I would be successful
- but have doubts that I would be successful
WroteBut it is possible.
P.S. This is not a correct example too, the determinant is zero. The sum of squares must be on all points.
Thank you for considering this
[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a1)),i,1,n)≡0[/MATH]
[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a2)),i,1,n)≡0[/MATH]
[MATH=eng]sum(((el(pp,i)-f(el(xx,i),a1,a2,a3))*diff((f(el(xx,i),a1,a2,a3)),a3)),i,1,n)≡0[/MATH]
It is a well known and maybe redundant to say, sorry - the first derivatives over three unknowns (a1,a2,a3) should be zero. The Jacobian of these three equations should not be zero (say, giving all xx different).
The problem is in derivatives, Jacobi matrix etc. (includes summation and quite large expressions). Whenever I tried to solve this root finding problem in SMath, finding derivatives, Jacobian etc. causes the main problem.
Anyway, could you please try to solve with this method the three above equations using your example function, but with more than three points.
Regards,
Radovan
P.S. I just saw that you added smz file as well. I might try myself ass well
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#12 Posted: 10/4/2012 9:54:18 PM
Radovan, I can't say something in your case. Yes, there is a problem with the Jacobian. I can't understand what exactly is the problem, so we turn to a simple example for now.
Draghilev's method. Finding roots. System 2 version 0.2.smz (7 KiB) downloaded 123 time(s).
Draghilev's method. Finding roots. System 2 version 0.2.smz (7 KiB) downloaded 123 time(s).
Russia ☭ forever, Viacheslav N. Mezentsev
1 users liked this post
Radovan Omorjan 10/5/2012 2:28:00 AM
#14 Posted: 10/5/2012 2:44:40 AM
Thank you uni for your time,
I also tried your simple example yesterday and was surprised that it worked well, but for some data worked well and for some other did not - as you mentioned.
I will try this new example as soon as your server become available (temporarily down at the moment)
By the way, I bumped many times into the derivative, gradient, Jacobian problem in SMath and almost always had to give it up. I even asked Andrey few times to introduce numerical differentiation in spite of the well known fact that numerical differentiation is prone to numerical errors. Calculating even derivatives (Jacobian is another nightmare) analytically is sometimes almost impossible and there is no other way than using some kind of numerical approximation. Therefore, when Jacobian is involved in some calculation - I always find myself unconfortable

Regards,
Radovan
EDIT: You are right - Pressing F9 several times can make it work. The error message was always "Action could not be performed with text" .
By the way, I even get the results of this function
[MATH=eng]f(x,a):sum((el(a,k)*x^{K-k}),k,1,K)+sin(x)[/MATH]
but after pressing F9 quite a lot of times.
I also tried your simple example yesterday and was surprised that it worked well, but for some data worked well and for some other did not - as you mentioned.
I will try this new example as soon as your server become available (temporarily down at the moment)
By the way, I bumped many times into the derivative, gradient, Jacobian problem in SMath and almost always had to give it up. I even asked Andrey few times to introduce numerical differentiation in spite of the well known fact that numerical differentiation is prone to numerical errors. Calculating even derivatives (Jacobian is another nightmare) analytically is sometimes almost impossible and there is no other way than using some kind of numerical approximation. Therefore, when Jacobian is involved in some calculation - I always find myself unconfortable
Regards,
Radovan
EDIT: You are right - Pressing F9 several times can make it work. The error message was always "Action could not be performed with text" .
By the way, I even get the results of this function
[MATH=eng]f(x,a):sum((el(a,k)*x^{K-k}),k,1,K)+sin(x)[/MATH]
but after pressing F9 quite a lot of times.
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#15 Posted: 10/5/2012 8:10:05 AM
Unfortunately, the plugin can't correctly translate all that much data with which it communicates with the Maple. Do not forget to delete the file mvr5.txt. Here you can see the language in which the plugin communicates with the Maple. And one more example. I increased the dimension of the problem and the number of points.
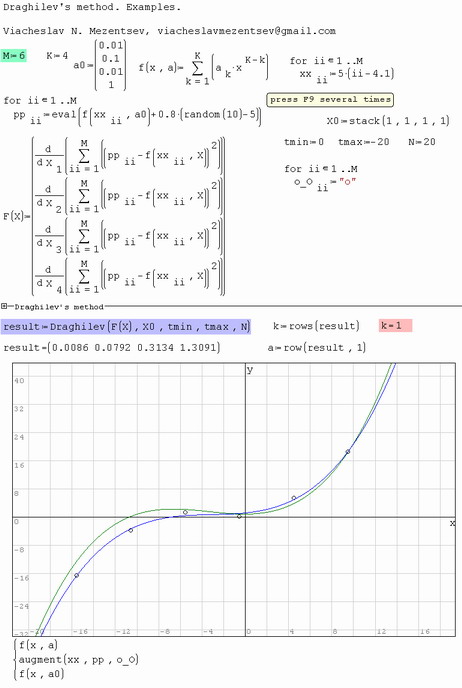
Russia ☭ forever, Viacheslav N. Mezentsev
1 users liked this post
Radovan Omorjan 10/5/2012 8:27:00 AM
#16 Posted: 10/5/2012 8:42:50 AM
Thank you uni,
Still pressing F9 lots of time is needed.
Wish you good luck in resolving this problem and improving the plugin .
.
I remember you mentioned that the real benefit SMath will have by developing its own symbolic engine. I hope that the SMath improvement of its engine will happen as well, and in not so a distant future.
Regards,
Radovan
P.S. A minor comment:
By the way, Is there any way that the plugin will follow the naming function convention in SMath (World, Europe). Just a simple example
[MATH=eng]maple(int(1/sqrt(1-x^2),x))=arcsin(x)[/MATH]
and there is actually World style (asin() instead of arcsin())
Still pressing F9 lots of time is needed.
Wish you good luck in resolving this problem and improving the plugin
I remember you mentioned that the real benefit SMath will have by developing its own symbolic engine. I hope that the SMath improvement of its engine will happen as well, and in not so a distant future.
Regards,
Radovan
P.S. A minor comment:
By the way, Is there any way that the plugin will follow the naming function convention in SMath (World, Europe). Just a simple example
[MATH=eng]maple(int(1/sqrt(1-x^2),x))=arcsin(x)[/MATH]
and there is actually World style (asin() instead of arcsin())
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#17 Posted: 10/5/2012 9:09:37 AM
Press F9 need to generate random numbers. I think that this should be on the expression where it is described (inside it). I get the result after every of 5-7 pushing. You can also increase the spread of the points (instead of a factor of 0.8 to take a little more).
Hmm. As I see it, in SMath used arc*() style, isn't it? (Russian interface) If Europe is different, I need to give a complete list of mathematical functions, where you need to make corrections, and three letters of the interface language (or just language name).
P.S. Radovan, I think that you need something like this: Nonlinear Regression II, Fitting a Curve to a Data Set with the New Gradient Operator
Hmm. As I see it, in SMath used arc*() style, isn't it? (Russian interface) If Europe is different, I need to give a complete list of mathematical functions, where you need to make corrections, and three letters of the interface language (or just language name).
P.S. Radovan, I think that you need something like this: Nonlinear Regression II, Fitting a Curve to a Data Set with the New Gradient Operator
Russia ☭ forever, Viacheslav N. Mezentsev
1 users liked this post
Radovan Omorjan 10/5/2012 9:40:00 AM
#18 Posted: 10/5/2012 11:09:44 AM
Hello uni
Actually, that is the all point . I am quite well acquainted with linear and nonlinear curve fitting in Mathcad. I also have it done for my students for years (in Mathcad and other software). The fact is that SMath does'nt have it o_o yet. For quite a while I am hopping that those things are going to be made in SMath by some users and plugins. The root solving plugin is developing by w3b5urf3r Non Linear Solvers (root-finding methods) - BDQRF, Bisection, Brent's, Broyden's, Newton-Raphson, Ridder's, Secant, Homotopy . There is no classical optimization procedure needed for nonlinear curve fitting - in that sense I was just trying Draghilev's method.
. I am quite well acquainted with linear and nonlinear curve fitting in Mathcad. I also have it done for my students for years (in Mathcad and other software). The fact is that SMath does'nt have it o_o yet. For quite a while I am hopping that those things are going to be made in SMath by some users and plugins. The root solving plugin is developing by w3b5urf3r Non Linear Solvers (root-finding methods) - BDQRF, Bisection, Brent's, Broyden's, Newton-Raphson, Ridder's, Secant, Homotopy . There is no classical optimization procedure needed for nonlinear curve fitting - in that sense I was just trying Draghilev's method.
To be honest, in order to replace Mathcad (Prime) and use SMath completely in my teaching, I need only few more things (like nonlinear curve fitting) but time is passing and I am still waiting o_o . I have enough time for that, but would like to be ASAP.
It is easily to find out that these few things are needed for majority of the engineering math and modeling problems. SMath's visual capabilities are very attractive for engineering applications.
- system of linear equations (SMath - should be improved)
- system of nonlinear equations (SMath - roots(), not good enough - plugin made by w3b5urf3r)
- system of first order ODE (SMath - plugin made by uni, improving appreciated)
- interpolation (SMath - included, should be improved)
- differentiation, integration (SMath - should be improved)
- linear and nonlinear curve fitting (SMath - not included, neither plugins made)
- 2D and 3D plotting (SMath - should be improved)
- units (SMath - quite good enough)
Unfortunately, in the present state I still do not quite understand how and why SMath is doing some things, I am often puzzled with it - and I do not like that feeling . In order to use it in my teaching I should understand it better. Unfortunately, that is still not the case.
. In order to use it in my teaching I should understand it better. Unfortunately, that is still not the case.
Regards,
Radovan
Wrote.S. Radovan, I think that you need something like this: Nonlinear Regression II, Fitting a Curve to a Data Set with the New Gradient Operator
Actually, that is the all point
To be honest, in order to replace Mathcad (Prime) and use SMath completely in my teaching, I need only few more things (like nonlinear curve fitting) but time is passing and I am still waiting o_o . I have enough time for that, but would like to be ASAP.
It is easily to find out that these few things are needed for majority of the engineering math and modeling problems. SMath's visual capabilities are very attractive for engineering applications.
- system of linear equations (SMath - should be improved)
- system of nonlinear equations (SMath - roots(), not good enough - plugin made by w3b5urf3r)
- system of first order ODE (SMath - plugin made by uni, improving appreciated)
- interpolation (SMath - included, should be improved)
- differentiation, integration (SMath - should be improved)
- linear and nonlinear curve fitting (SMath - not included, neither plugins made)
- 2D and 3D plotting (SMath - should be improved)
- units (SMath - quite good enough)
Unfortunately, in the present state I still do not quite understand how and why SMath is doing some things, I am often puzzled with it - and I do not like that feeling
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
1 users liked this post
Вячеслав Мезенцев 10/5/2012 11:14:00 AM
#19 Posted: 10/5/2012 11:29:00 AM
Radovan, if you want to understand it better, then you need to try to write the interpreter symbolic computation by yourself. It's not that hard. There is even an introductory book - Computer Algebra with SymbolicC++.
P.S. On the picture is a simple example of the SMath-style calculator, which is written in VB6: sources (draft, russian).

P.S. On the picture is a simple example of the SMath-style calculator, which is written in VB6: sources (draft, russian).
Russia ☭ forever, Viacheslav N. Mezentsev
#20 Posted: 10/5/2012 12:35:51 PM
Sorry, uni - I did not make myself clear enough 
I did not mean by "understanding" to know how SMath is working in programming sense in order to make plugins, or things like that. I am to old for that and it is beyond my capabilities. I was just thinking to understand it from the SMath user point of view - in order to use it like a math and engineering tool. I want to use it in order to solve my standard problems that I have in my class, and to understand pretty well how to solve those problems by using SMath. Unfortunately, I am to often getting confused by struggling with its own problems - like symbolic engine, its optimization feature etc. I do not often understand SMath behavior, can not often rely on its results etc. Maybe a much better explanation of our frustrations at the moment gave Martin Kraska (mkraska) in its recent post Post by mkrska.
Quite similar frustrations had and still have Mathcad "oldtimers", but it can not be compared with SMath.
From my point of view, SMath is very, very close to the point of software I always wanted - but it is still not there
Regards,
Radovan
I did not mean by "understanding" to know how SMath is working in programming sense in order to make plugins, or things like that. I am to old for that and it is beyond my capabilities. I was just thinking to understand it from the SMath user point of view - in order to use it like a math and engineering tool. I want to use it in order to solve my standard problems that I have in my class, and to understand pretty well how to solve those problems by using SMath. Unfortunately, I am to often getting confused by struggling with its own problems - like symbolic engine, its optimization feature etc. I do not often understand SMath behavior, can not often rely on its results etc. Maybe a much better explanation of our frustrations at the moment gave Martin Kraska (mkraska) in its recent post Post by mkrska.
Quite similar frustrations had and still have Mathcad "oldtimers", but it can not be compared with SMath.
From my point of view, SMath is very, very close to the point of software I always wanted - but it is still not there
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
-
 New Posts
New Posts
-
 No New Posts
No New Posts
