I have made a plugin to calculate big integers.
Actually I had coded it under SMath but it is way slow with very big numbers.
So I have made it a plugin which is coded with c#.
It gets the decimal as string, gives the result as string.

Do you think this would be useful for some instances?

Regards

biginteger_compiled.7z (4 KiB) downloaded 103 time(s).
source_code.7z (6 KiB) downloaded 98 time(s).
System.Numerics.7z (43 KiB) downloaded 97 time(s).

The big number code exists in Mathcad.
IMHO, useless or unknown use, whereas all functions are 15 D.
Forget my comment. Try to apply to the example posted some days ago.

Wrote

Try to apply to the example posted some days ago.

... that one

Critical error.sm (2 KiB) downloaded 57 time(s).

Well Jean, you are free not to use it if I publish it.
Here is the answer of you question.

the logic is very simple:
it is much better to have it and not use it
than to need it and not have it

great job overlord

I Agree completely with the previous post. Well done Overlord and Keep up the good work.

Best Regards

Franco

Wrote

Well Jean, you are free not to use it if I publish it.

That is not the matter. Smath has its own big number invisible code.
It displays max 15 digits but there is more internal.
Remember, some residuals imaginary i^-31.
A recent example is McCabe-Thiele.
Conserving the rounded 15 'K' does not plot "No real roots"
By conserving the 'K' in native Smath invisible big number, solver works
and we get the classical McCabe-Thiele graph [zizag style].
In Mathcad [you are familiar ?]
float 40 x^0.5 you get only 21 decimals ... ^0.5 is undefined
float 40 x^½ you get 40 decimals ^½ is defined
Just a nuance that puzzled many Mathsoft collabs.
The ratio of my big division is fractional, from reduced expansion.
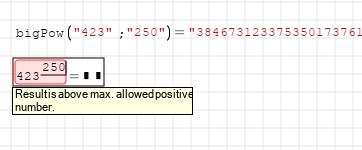
Would that help solving the error "above max allowed ..." ???
Can you demonstrate an Engineering example not solvable otherwise ?
i.e: not solvable otherwise than via big number.
Isn't what eval(,) does in some way(s) ?
In CAS, constants are stored 40 decimals [sqrt(2), ln(2), pi ...]
Most interesting ... Jean.

... by same token:
"Try-on error", what is the throw away [error] criterium ?

... what about complex numbers ?

Wrote

Would that help solving the error "above max allowed ..." ???
Can you demonstrate an Engineering example not solvable otherwise ?

Big integers are used generally in encryption,
mathematical calculations where high-value numbers are handled,
image processing programs, financial analysis applications, etc.
Where you need big number data handling you can use big integer.

And notice, this is Big Integer Library.
It will help "above max allowed" if only variables and answer are integers.
What you are asking is Big Fractions Library.
Maybe someday I will implement fractions too, if I can.
No promises here.

Regards

You will like my 3 big numbers, in fact just peanut size 2112
Enjoy ... Jean

BigNumber.sm (218 KiB) downloaded 63 time(s).

Then you will like this library even more.
This functions can calculate and show
1.68 million digits in a minute.
12345678901234567890123456789^60000
Not so bad huh?

Regards

Wrote

I have made a plugin to calculate big integers.

Hi. It looks great. Maybe you can found interesting this post: https://math.stackexchange.com/questions/514/conjectures-that-have-been-disproved-with-extremely-large-counterexamples

This other is about some students who could not solve a problem that their teacher had asked them, and had good reasons not to do it. He acquired a bit of fame over time: https://math.stackexchange.com/questions/402537/find-integer-in-the-form-fracabc-fracbca-fraccab

Best regards.
Alvaro.

Wrote

Do you think this would be useful for some instances?

I can't see any useful instance(s) for productive Smath projects,
maybe except for some distractive conjectures [Diophantine style].
Native Smath 6179 comes with Maple big Number expansion.
Problem is that if too big, will not evaluate ... Ah !
The attached example does not complain, just great for purpose.
Maybe, I don't understand your proposal. Big Number does not self create.
Don't they result from a creator to rescue the Grand Creator ?
Cheers ... Jean.

Page3 Cabe J_frac.sm (28 KiB) downloaded 56 time(s).

Wrote

I can't see any useful instance(s) for productive Smath projects.
Native Smath 6179 comes with Maple big Number expansion.
Maybe, I don't understand your proposal. Big Number does not self create.

Check the example below, the number has been directly copied from your example.
If you +1 that number, SMath (and maple plugin) can't tell the difference.
They are same to SMath (which in most cases won't matter) but not to big number calculation.
I understand, most of times it won't matter but what if it matters on special occasions?

It is clear you can't see its usefulness.
Maple support is crippled by SMath conversion, Davide or Martin mentioned about this.
And it is clear you don't understand my proposal.

Especially when everyone says "good idea" you insist on opposite.
Or you perseveringly try to divert the subject out of context.
Or you tenaciously try to advert your worksheets, which are irrelevant with subject.
This behavior is not helpful, you are just being rude.
You are doing this mostly on my posts by the way.
If you have any grudge on me lets clear it out now.

Wrote

Especially when everyone says "good idea" you insist on opposite.

I just want an Smath project that can't be solved without.
Designers will surely appreciate the void under the hood.

Wrote

Wrote

Especially when everyone says "good idea" you insist on opposite.

I just want an Smath project that can't be solved without.
Designers will surely appreciate the void under the hood.

Clearly you have no knowledge on arbitrary precision.
People are programming and using it since beginning of electronic computing.
Start from here https://en.wikipedia.org/wiki/Arbitrary-precision_arithmetic

Some other calculation programs have it; wolfram has it, mathematica has it if you want example.
There is no reason for SMath not having this. Compiled plugin is working what it is committed.
I repeat again, you have your freedom not to install it. You wanting a project is irrelevant.
You are not an authority to decide what is beneficial what is not. Please don't continue this attitude.

Regards

Wrote

Clearly you have no knowledge on arbitrary precision.
People are programming and using it since beginning of electronic computing.

The first computer I was involved 1962 was triode system.
Around this time, big war between the French Bull and Kennedy.
France refused to share Bull, which Bull now consumes a Nuclear Power Plant.
In 1970, I punched Fortran cards [personal & Employer]. I have Mathematica.
No demonstration how Smath is missing ... end of it.

Wrote

The first computer I was involved 1962 was triode system.
Around this time, big war between the French Bull and Kennedy.
France refused to share Bull, which Bull now consumes a Nuclear Power Plant.
In 1970, I punched Fortran cards [personal & Employer]. I have Mathematica.
No demonstration how Smath is missing ... end of it.

You don't get it, I have no obligation to prove or demonstrate you the usage of arbitrary precision.
It is there, it is important, every major programming language has it. Pi calculation is there, cryptology is there, Riemann zeta function is there, high precision Mandelbrot rendering is there; go find yourself usage of it.
If you can't find or don't need it this doesn't give you word to say "no one need it". You are just a selfish mean who thinks "I don't need it then no one should".
I don't care what have you done, what Fortran card you punched in which year. You have no authority on me, you can't tell me what to do or anyone. Heck, while you are punching cards people were trying to compute with big numbers.
"A Statistical Study of the Randomness Among the First 10,000 Digits of Pi"
Thankfully computer science had people opposite of your "we don't need this" thoughts and now we have these technologies. If it was up to you we would still punching cards.
I don't want to see your gibberish under my posts ever again, end of it.

Wrote

...
You don't get it, I have no obligation to prove or demonstrate you the usage of arbitrary precision.
...

You don't, I agree, with that and with all of what you say. Neither do I, but since I already did, I can dig a little deeper. Here are some examples of what happens if rounding errors are not taken into account: http://catless.ncl.ac.uk/Risks/search?query=rounding

Some examples listed there are well known and are in every presentation by a computer lab teacher ( http://indico.ictp.it/event/8344/session/50/contribution/207/material/slides/0.pdf ).

The library can be used both to perform calculations directly on some sensitive issues that require a thorough review of the calculations, or to check the stability of the numerical method used. Personally, I do not analyze rounding errors that way, but rather I use variable precision arithmetic or interval algebra ( https://www.maplesoft.com/applications/view.aspx?SID=1389 ). The latter I can link directly to the method of propagation of errors through gradients, which I certainly applied in practice, being the only one available in addition that I understood how to interpret an old standard for calibrating atmospheric storage tanks, which I must thank my teacher in the physics laboratory , as she rejected reports that did not have the values ​​and the associated error. Also, SMath sys() behavior can use for do something like the maple's IntervalArtithmetic package.

Best regards.
Alvaro.