Wrote

The parameterization by Draghilev method.The starting point is taken near the bifurcation point (0,0).

Just a very little modifications: using norme(J) and the SMath ability for handling undefined parameters.


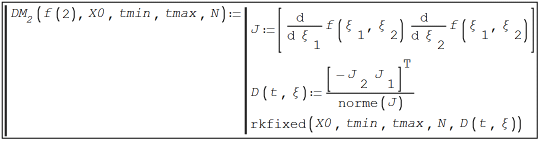
ContourTifoleum.sm (16 KiB) downloaded 78 time(s).

Best regards.
Alvaro.

Thank you, Alvaro. The norme function simplifies the code and reduces the calculation time.
Example of using norme when solving ODE

LorenzPointsAreEquidistantc.sm (6 KiB) downloaded 83 time(s).

Hi Ber. I don't remember to read nothing in the literature about equally spaced points in the numerical solution of the ode, except for the opposite: adaptive steps, but referring for the time variable, not the X,Y,Z solution points. About how you apparently get the same distance between solution points, i.e. sqrt(X^2+Y^2+Z^2), I guess that the background theory must to be in the Draghilev method and how the solution (X,Y,Z) is obtained from the differential equation. You have a very interesting point for investigate and publish about it.

I try to investigate the relationship between the symbolic ode solution and the paramatrization, but the symbolic solutions are quite complicated, and I don't have simple examples.

Apparently the distance between the points is 1 (guess can be easily proved because you divide by the norme the system), and this seems to provide more stable numerical solutions for the system (can be applied here Lyapunov's theorems?)



Unfortunately in this example I introduce the factor 1/1000 for avoid numerical over max limit error for the case without norme.

Best regards.
Alvaro.

Wrote

The parameterization by Draghilev method.The starting point is taken near the bifurcation point (0,0).

Thanks Ber7, gorgeous
For this particular Trifolium, once created it is easy to collect
as many as desired to any scale corresponding to Draghilev 'a'
The great tool here, is the bidirectional fmesh(f(x),x0,x1,mesh)

Cheers ... Jean

2D Parametric Plot [Create Trifolium].sm (31 KiB) downloaded 83 time(s).

Thank you Jean, I suggest a small change in the animation.
TrifoliumAnim.sm (24 KiB) downloaded 73 time(s).

Wrote

I suggest a small change in the animation.

Thanks Ber7 ... even more compacted.
Trifolium:=stack(b1,b2,b3,b4) from inversing f4(x) <= f3(x).

0Anim Trifolium [Windmill Ber7].sm (25 KiB) downloaded 70 time(s).

Graph of implicit function with bifurcation point (Problem on
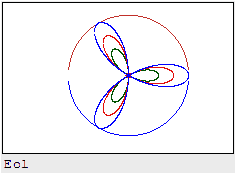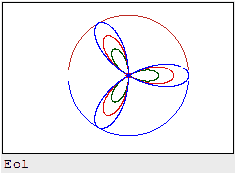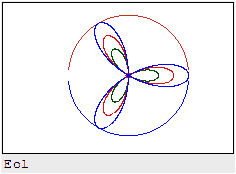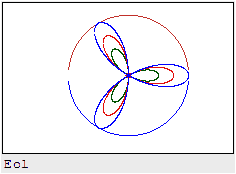
the calculation of the arch)
https://en.smath.info/forum/yaf_postst7262_Solution-of-nonlinear-equations-by-Draghilev-method-in-Engineering.aspx

The graph consists of three curves that occur at the bifurcation point.
1. Find the coordinates of the bifurcation point
2.The starting point for each of the three graphs is taken near the bifurcation point
3. Build graphics by Draghilev method

Point Bifurcation.sm (38 KiB) downloaded 75 time(s).

Wrote

The graph consists of three curves that occur at the bifurcation point.
1. Find the coordinates of the bifurcation point
2.The starting point for each of the three graphs is taken near the bifurcation point
3. Build graphics by Draghilev method

Thanks Ber7.
This version works fine compared to the previous "arca" that never stopped pedaling .
By same token, I'm puzzled by the Lagrange points. Where those contours come from ?

Joan

from Wikipedia it is stated that they are involved in Astronomy and that for 2 large bodies there are 5 of these points so I guess that your pictures/worksheet refers on how to calculate them all(their positions).

https://en.wikipedia.org/wiki/Lagrangian_point

Best regards

Franco

Wrote

Thank you, Alvaro. The norme function simplifies the code and reduces the calculation time.
Example of using norme when solving ODE

dn_GearsBDF is nearly ½ time. I think its Lorentz

Maple, Draghilev's method. The inverse problem of kinematics. For those who want to try hard and to do better in SMath.

Wrote

hose who want to try hard and to do better in SMath.

Thanks for the suggestion. My head is not oblate like Extraterrestrials !

Wrote

. I don't remember to read nothing in the literature about equally spaced points in the numerical solution of the ode, except for the opposite: adaptive steps, but referring for the time variable, not the X,Y,Z solution points. About how you apparently get the same distance between solution points, i.e. sqrt(X^2+Y^2+Z^2), I guess that the background theory must to be in the Draghilev method and how the solution (X,Y,Z) is obtained from the differential equation. You have a very interesting point for investigate and publish about it.
Apparently the distance between the points is 1 (guess can be easily proved because you divide by the norme the system), and this seems to provide more stable numerical solutions for the system (can be applied here Lyapunov's theorems?)

Best regards.
Alvaro.

An article about the effectiveness of the solution of the system diff. equations for parameterization integral curve through arc length
Russiy.pdf (607 KiB) downloaded 89 time(s).

Wrote

Wrote

. I don't remember ...

An article about the effectiveness of the solution of the system diff. equations for parameterization integral curve through arc length
Russiy.pdf (607 KiB) downloaded 89 time(s).

Thanks for the paper. Now you found the keywords for this point, which seems to be "Arc Length Method". This give only 79 results at google search:


Results are related with mechanical engineering for finite elements analysis. From the first result, having this attached file: https://scholar.harvard.edu/files/vasios/files/ArcLength.pdf




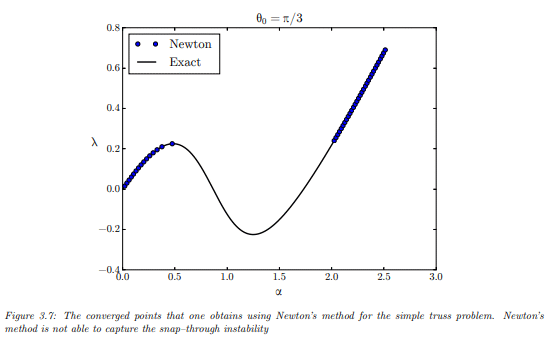
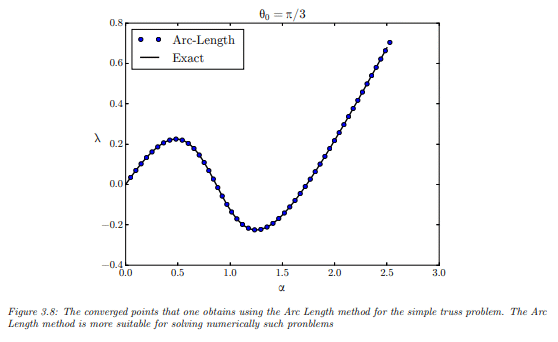
But actually I don't find any appointment nor observation that solution points are equally spaced. Notice that It could be some "obvious" point for, given f(t,x,x' ) = 0, plot for x(t) it's equally spaced if one transform it to f(s,x,x' ) with s as the arc length. But it's immediate for me that the plot for the state space (x,x' ) seems to be equally spaced too, as in some smath examples here in this topic.

Also, for the observation that can apply Lyapunov theorems about stability of solutions, there are some references in the 79 google's search results. The application here of Lyapunov is related about the stability of the found solutions, because authors using the parametrization along the arc length for ill conditioned systems.

Wrote

. Apparently the distance between the points is 1 (guess can be easily proved because you divide by the norme the system), and this seems to provide more stable numerical solutions for the system (can be applied here Lyapunov's theorems?)

Best regards.
Alvaro.

Finding Minimum Distanceof a Point from Curve
(with Draghilev method)


MinDistDragilev.sm (23 KiB) downloaded 75 time(s).

Wrote

Finding Minimum Distance of a Point from Curve

Thanks Ber7 ... works fine.

Distance from point to implicit curve(with al_nleqsolve)
A thick red line is the normal to the curve at point a.


FindDist.pdf (243 KiB) downloaded 69 time(s).
FindDist.sm (72 KiB) downloaded 81 time(s).

Refined the algorithm and added examples
DistMod.sm (51 KiB) downloaded 77 time(s).

Wrote

Refined the algorithm and added examples

Thanks Ber7,
looks interesting but couldn't doctor SS 6179.

How the algorithm works.
Each time you press F9, we set the new position of point A

Animat.sm (21 KiB) downloaded 70 time(s).