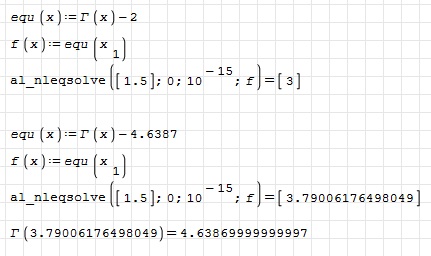Gamma Functions

#1 Posted: 6/7/2021 5:07:11 PM

554 likes in 1333 posts.

Group: Moderator

Gamma function,
Lower Incomplete Gamma function,
Upper Incomplete Gamma function,
with almost instant speed and high precision.

Regards

gamma.sm (34 KiB) downloaded 55 time(s). <---- least accurate
gamma_r2.sm (11 KiB) downloaded 54 time(s).
gamma_r3.sm (11 KiB) downloaded 53 time(s).
gamma_r4.sm (13 KiB) downloaded 51 time(s).
gamma_r5.sm (11 KiB) downloaded 53 time(s).
gamma_r6.sm (17 KiB) downloaded 48 time(s).
gamma_r7.sm (28 KiB) downloaded 58 time(s).
gamma_r8.sm (31 KiB) downloaded 44 time(s).
gamma_r9.sm (36 KiB) downloaded 86 time(s). <----imaginary numbers added

#2 Posted: 6/8/2021 2:57:24 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote
Thanks, will explore.

Main limitation is smath floating points.
Python gives much more accurate results with same algorithms.
Try the other one for gamma calculation.

gamma_r2.sm (11 KiB) downloaded 54 time(s).

#3 Posted: 6/8/2021 7:21:30 PM

Jean Giraud

983 likes in 6866 posts.

Group: User

Wrote
Try the other one for gamma calculation.

round(■ ,■ ,■ ) ... undefined
H.T.Davis [Abramowitz & Stegun] -> very objective.
In the mean time I'm finishing two superb applications examples
... examples based on your first Gamma(a,x) version,
Thanks for that one, gorgeous ... Jean.

gamma_r2 [H.T.Davis].sm (57 KiB) downloaded 45 time(s).

#4 Posted: 6/8/2021 7:55:03 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote

Wrote
Try the other one for gamma calculation.

round(■ ,■ ,■ ) ... undefined
H.T.Davis [Abramowitz & Stegun] -> very objective.
In the mean time I'm finishing two superb applications examples
... examples based on your first Gamma(a,x) version,
Thanks for that one, gorgeous ... Jean.

Undefined because you have an old version of smath.
Round(#,#,#) is not parsed through your program.
Use trunc() instead. And with more constants.

gamma_r3.sm (11 KiB) downloaded 53 time(s).

#5 Posted: 6/8/2021 8:34:03 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Technically this should be the most accurate one.

gamma_r4.sm (13 KiB) downloaded 51 time(s).

#6 Posted: 6/8/2021 9:34:29 PM

Jean Giraud

983 likes in 6866 posts.

Group: User

As offered ... two applications.
Now, the old Rooster is going in the bed marmite ... Jean.

gamma(a,x) Applications.sm (23 KiB) downloaded 55 time(s).

#7 Posted: 6/8/2021 10:08:00 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote
As offered ... two applications.
Now, the old Rooster is going in the bed marmite ... Jean.

gamma(a,x) Applications.sm (23 KiB) downloaded 55 time(s).

I suggest you to change gamma function with gamma_r4.
It is 3 times faster and much more precise.

#8 Posted: 6/9/2021 1:46:58 PM

Jean Giraud

983 likes in 6866 posts.

Group: User

Wrote
I suggest you to change gamma function with gamma_r4.
It is 3 times faster and much more precise.

Thanks for gamma_r4
1. NO gain timing both applications
2. gamma_r4 Does NOT solve ... first version solves.

#9 Posted: 6/9/2021 2:06:13 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote
Thanks for gamma_r4
1. NO gain timing both applications
2. gamma_r4 Does NOT solve ... first version solves.

Speed may differ between linux and windows.
gamma_r4 is faster 3 times in linux.
What do you mean by 'does not solve'?
How should this page look like?

gamma(a,x) Applications.pdf (125 KiB) downloaded 56 time(s).

#10 Posted: 6/9/2021 2:19:23 PM

Jean Giraud

983 likes in 6866 posts.

Group: User

Wrote
What do you mean by 'does not solve'?

#11 Posted: 6/9/2021 2:36:55 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote

Wrote
What do you mean by 'does not solve'?

I think this is the same bug I mentioned earlier. Some functions don't like to be in another function.

Solution was to put a line but that method is not working in this case.

@Andrey or @Davide has to look at this.

#12 Posted: 6/9/2021 4:03:46 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote
1. NO gain timing both applications

Latest version is faster about 4 times.

#13 Posted: 6/9/2021 4:23:05 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote

Wrote
What do you mean by 'does not solve'?

It solves, not with conventional methods.
They tend to give errors, not gamma_r4's fault.
alglib is the answer, it usually gives result.

#14 Posted: 6/9/2021 9:50:11 PM

Jean Giraud

983 likes in 6866 posts.

Group: User

Wrote
It solves, not with conventional methods.
They tend to give errors, not gamma_r4's fault.
alglib is the answer, it usually gives result.

Good rescue ... OK.
As it looks, sr4 resides at the kernel level.
Thus, it plots but not solve(,,,,)
because not scalar wrt 'x' for the solve bloc.

#15 Posted: 6/9/2021 10:06:36 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote
Good rescue ... OK.
As it looks, sr4 resides at the kernel level.
Thus, it plots but not solve(,,,,)
because not scalar wrt 'x' for the solve bloc.

Nope, not related with kernel, blocks, scalability, etc.
It is probably a bug of solve(), roots(), FindRoot().
Gamma Function has nothing to do with it.
Even very simple ones suffer from this too.
Check below.

#16 Posted: 6/9/2021 10:22:56 PM

overlord

554 likes in 1333 posts.

Group: Moderator

It seems solve(), roots(), FindRoot() doesn't like if statements.
I have updated the bugreport in Bugs and Problems > solve() bug.
Using cases() seems to solve the issue. Check the sample below.

gamma_r5.sm (11 KiB) downloaded 53 time(s).

#17 Posted: 6/10/2021 11:16:16 AM

Jean Giraud

983 likes in 6866 posts.

Group: User

Wrote
Check the sample below

Doctored version confirmed.

#18 Posted: 6/10/2021 10:56:05 PM

overlord

554 likes in 1333 posts.

Group: Moderator

gamma_r5 has a serious flaw. It can't calculate a<0.5.
My bad, should check it carefully. Corrected page is below.
Refactored so it is faster, also get rid of recursive call.
I had to get around some smath bugs with line, if/cases, recursive.
Correlation of them gives weird errors.
Hope this version solves all issues and be the last one.
I know I have flooded this topic too much, sorry for inconvenience.

Regards

gamma_r6.sm (17 KiB) downloaded 48 time(s).

PS: gamma for negative non-integer values support corrected

#19 Posted: 6/11/2021 10:16:24 AM

Jean Giraud

983 likes in 6866 posts.

Group: User

Wrote
I know I have flooded this topic too much

You may not like my verdicts:
1. on-line faster has no or little interest, neither up ^307.
2. Your first version runs fine the two applications.
3. The champion is the long time ago published Alvaro Γ(x)
4. for these two applications [2] & [3] are same
but => [3] drops timing [2] from 24 s down 18 s
The drop in timing results from Alvaro Γ(x)
running at the kernel scalar level.
BTW, my original H.T. Davis sanity Mathcad & Alvaro Γ(x)
By same token, thanks Alvaro for your Γ(x).
Cheers ... Jean

Maths Special Gamma(a,x) Incomplete APPLICATIONS [Alvaro G(x)].sm (26 KiB) downloaded 52 time(s).

#20 Posted: 6/11/2021 12:45:20 PM

overlord

554 likes in 1333 posts.

Group: Moderator

Wrote

Wrote
I know I have flooded this topic too much

You may not like my verdicts:
1. on-line faster has no or little interest, neither up ^307.
2. Your first version runs fine the two applications.
3. The champion is the long time ago published Alvaro Γ(x)
4. for these two applications [2] & [3] are same
but => [3] drops timing [2] from 24 s down 18 s
The drop in timing results from Alvaro Γ(x)
running at the kernel scalar level.
BTW, my original H.T. Davis sanity Mathcad & Alvaro Γ(x)
By same token, thanks Alvaro for your Γ(x).
Cheers ... Jean

Maths Special Gamma(a,x) Incomplete APPLICATIONS [Alvaro G(x)].sm (26 KiB) downloaded 52 time(s).

1. 10^308 feature added for fully use IEEE capability.
2. gamma_r6 runs every possible applications.
3. don't want to disrespect, Alvaro's is a single line awesome code.
4. mine has same algorithm with more features, with faster calculation.
4. gamma_r6 is faster from gamma_r2 and gamma_r3 while trying to have all feature.

gamma_r6_app.sm (33 KiB) downloaded 62 time(s).

Here is a side by side comparison with Alvaro's algorithm with mine.
On linux, gamma_r6 is faster about 20 percent.

Show Spoiler

SMath

Gamma Functions

Gamma Functions - rapid speed with precision - Messages

SMath Forum

Gamma Functions - rapid speed with precision - Messages