In the same way, you can add points to a triangle.

Wrote

In the same way, you can add points to a triangle.

Thanks again. You should know me: if the code is shorter, there are always several good reasons to say that it is better than the longer ones. Surely inefficient, but efficiency is often overrated.

In the traces menu of XYPlot, you have for the LineStyle.Method the options (Lines, Splines, Labels, etc.) If you add there the value "Polygon" maybe you can simplify the input for fill a region. In such case, the LineStyle.Pattern and LineStyle.Thiknes fields could represent the values for the for the border of the region, or maybe the values under the Symbol.Style fields, I don't see which one could be better. Or maybe "Polygon" goes under the field LineStyle.Pattern.

I don't know if a register for color transparency would be missing either.

BTW the goal is to enable the user to fill a region and mark its border by specifying only the points of the region once and as a simple matrix of XY values.

In any case, the notation you already have would not be touched, since it works very well. It would be very impractical to have to program the traces to represent a surface or vectors with changing colors if the current notation is lost.

Best regards.
Alvaro.

Hi Alvaro and others.

The following is my way of utilising the fact that u/v equals c/b, and since I can apply the cosine-relations on the 3 related triangles, I get the needed 4. equation from u+v=a and u/v=c/b.
After some trials it turned out, that "FindRoot" with the NonlinearSolvers plugin installed, could solve the 4 unknowns in 4 equations (which was my initial idea and problem). I have tried the method on several triangles with succes.
I would very much like a comment.

Best wishes
Søren.

p.s. My last problem with this triangle-thing is a way to construct it (like in the old days) using only pen, paper, ruler and compass - no computer!

File not found.File not found.

Here is a version with two unknowns.

Triangle.sm (20 KiB) downloaded 76 time(s).

One more example.

Wrote

... p.s. My last problem with this triangle-thing is a way to construct it (like in the old days) using only pen, paper, ruler and compass - no computer! ...

Hi Søren. Here the procedure with only ruler and compass, perhaps with the addition of an angle protractor and a square, to simplify our lives, and an auxiliary geometric construction would remain to be carried out to find the radius of the circle with center F and radius given by (h+√(h^2+8*OB*EF))/2, where h, OB and EF are known, and since it is quadratic, it can also be constructed using only a ruler and compass.

geom-scb-anim.sm (33 KiB) downloaded 58 time(s).



Best regards.
Alvaro.

Possible alternatives

P.S. Region(β,u) := (0<β<π Λ 0

A little shorter

Triangle (uni).sm (15 KiB) downloaded 58 time(s).

Trigonometric and root free, exact version, also using the new capabilities of XYPlot.

geom-scb-new-xyplot.sm (26 KiB) downloaded 61 time(s).



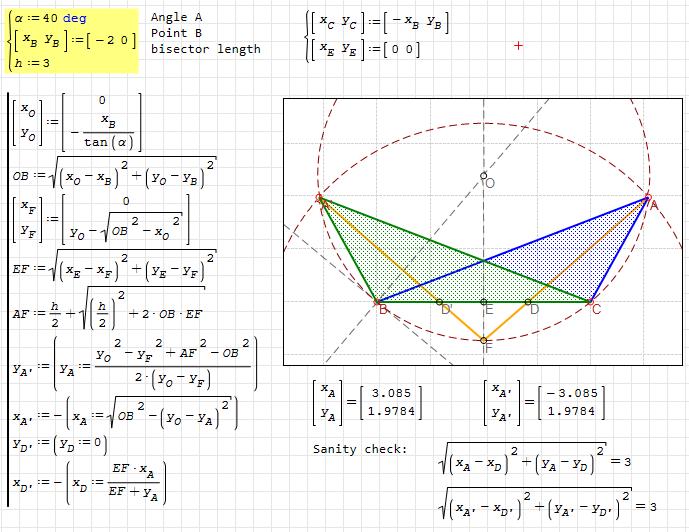
Best regards.
Alvaro.

Wrote

p.s. My last problem with this triangle-thing is a way to construct it (like in the old days) using only pen, paper, ruler and compass - no computer!

Here is a method I use to construct this triangle by trial and error, with "digital pen, paper, ruler and compass"


?si=plmK5j0jQs1Uvhtx

Best,

Oscar