1 страниц (19 вхождений)
plot a function - Сообщения
#1 Опубликовано: 04.12.2019 15:08:53
Hello everyone!
I have difficulty plotting the function c which depends on the derivatives of two functions which in turn depend on the parameter t.
Could anyone help me? This in the smath file.. curvatura.sm (11 КиБ) скачан 65 раз(а).
Thank you so much
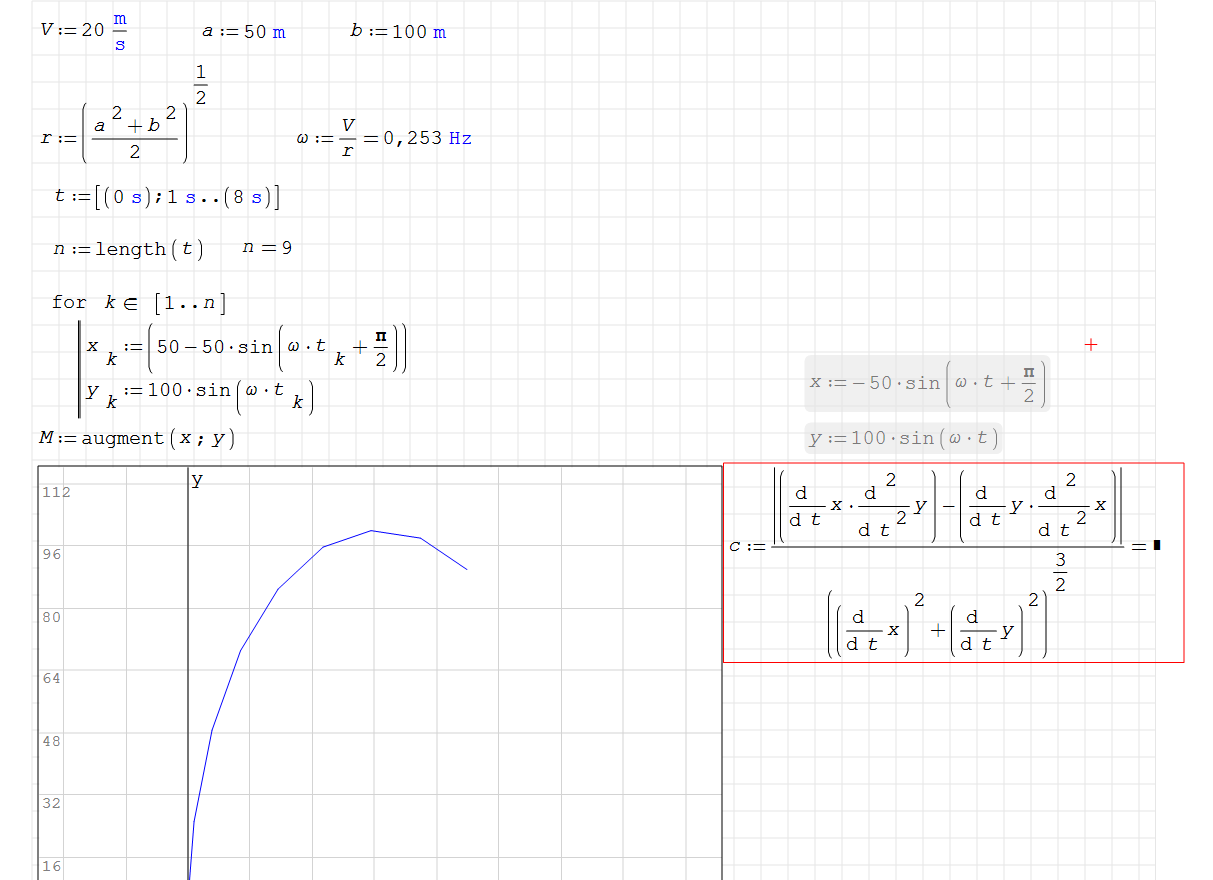
I have difficulty plotting the function c which depends on the derivatives of two functions which in turn depend on the parameter t.
Could anyone help me? This in the smath file.. curvatura.sm (11 КиБ) скачан 65 раз(а).
Thank you so much
#2 Опубликовано: 04.12.2019 17:37:09
WroteHello everyone!
I have difficulty plotting the function c which depends on the derivatives of two functions which in turn depend on the parameter t...
Maybe this is what you want...
... and the .sm file: curvatura1.sm (9 КиБ) скачан 81 раз(а).
#3 Опубликовано: 04.12.2019 18:19:46
WroteCould anyone help me ?
To plot both systems ... Jean
curvatura.sm (11 КиБ) скачан 91 раз(а).
Maths Tangent.sm (91 КиБ) скачан 92 раз(а).
#4 Опубликовано: 05.12.2019 08:37:36
thank you very much for your help, I hope I have no more problems
#5 Опубликовано: 05.12.2019 11:20:31
Wrotethank you very much for your help, I hope I have no more problems
You´re welcome.
It's okay to ask, because you express the need to know. It is better to ask than keep silence
#6 Опубликовано: 06.12.2019 09:21:28
Thank you very much for the availability.
But I need more help.
How can I draw the tangent line to the equation in parametric form?
this is the file … curvatura2.sm (12 КиБ) скачан 74 раз(а).
But I need more help.
How can I draw the tangent line to the equation in parametric form?
this is the file … curvatura2.sm (12 КиБ) скачан 74 раз(а).
#7 Опубликовано: 06.12.2019 12:48:15
Hi Ale. Here, some ways.
curvatura3.sm (25 КиБ) скачан 83 раз(а).
curvatura4.sm (20 КиБ) скачан 82 раз(а).
Best regards.
Alvaro
curvatura3.sm (25 КиБ) скачан 83 раз(а).
curvatura4.sm (20 КиБ) скачан 82 раз(а).
Best regards.
Alvaro
1 пользователям понравился этот пост
sergio 06.12.2019 17:23:00
#8 Опубликовано: 06.12.2019 13:08:58
WroteThank you very much for the availability.
But I need more help.
How can I draw the tangent line to the equation in parametric form?
For the Tangent over C(t), it will follow the scalar rules
of the document Tangent.sm posted before.
The Tangent over the parabola is another business.
Smath does not derive linterp(x) as it is NOT a function
only an interpolation. This project and lot more are
rescued via Infinitesimal Analysis [dates back before CAS].
For that particular typical user point of tangency, OK.
You may want to experiment more .
Don't mind to see noisy curvature [disabled in collapsed].
Chers ... Jean.
curvatura2 Copy.sm (30 КиБ) скачан 68 раз(а).
#9 Опубликовано: 06.12.2019 13:16:01
Thanks for the answers.
But if I wanted to find the tangent to the curve when the parameter t changes, how should I do?
But if I wanted to find the tangent to the curve when the parameter t changes, how should I do?
#10 Опубликовано: 06.12.2019 14:05:01
WroteThanks for the answers.
But if I wanted to find the tangent to the curve when the parameter t changes, how should I do?
Do you mean the envelope, all the tangents for the range en T?
curvatura5 - envelope.sm (23 КиБ) скачан 81 раз(а).
Best regars.
Alvaro.
1 пользователям понравился этот пост
sergio 06.12.2019 17:19:00
#11 Опубликовано: 06.12.2019 14:55:53
WroteHi Ale. Here, some ways.
Thanks Alvaro ... superb/saved ... Jean
#12 Опубликовано: 06.12.2019 15:02:35
#13 Опубликовано: 06.12.2019 22:48:04
Your project has been refactored strictly on discrete.
OK, you have functions but life is from collected data.
Collected data are always noisy from the quantization,
a small amount of Gaussian Ksmooth is often sufficient.
Ksmooth being applied before cinterp
As exemplified, cinterp is the best interpolator for
a clean curvature plot from infinitesimal maths.
I don't understand what your were attempting c(t) last module.
Please, don't hesitate for more.
Cheers ... Jean
Maths Tangent Data Set Copy.sm (36 КиБ) скачан 72 раз(а).
OK, you have functions but life is from collected data.
Collected data are always noisy from the quantization,
a small amount of Gaussian Ksmooth is often sufficient.
Ksmooth being applied before cinterp
As exemplified, cinterp is the best interpolator for
a clean curvature plot from infinitesimal maths.
I don't understand what your were attempting c(t) last module.
Please, don't hesitate for more.
Cheers ... Jean
Maths Tangent Data Set Copy.sm (36 КиБ) скачан 72 раз(а).
1 пользователям понравился этот пост
sergio 07.12.2019 07:36:00
#14 Опубликовано: 06.12.2019 23:22:41
WroteYour project has been refactored strictly on discrete.
O
.... more maths are coming:
cumulative integration, arc length
derivative you already have it from last attachment.
#15 Опубликовано: 07.12.2019 06:12:23
Thank you very much for the help, I appreciate it very much.
I hope to be able to continue alone.
kind regards
I hope to be able to continue alone.
kind regards
#16 Опубликовано: 07.12.2019 10:48:24
WroteThank you very much for the help, I appreciate it very much.
I hope to be able to continue alone.
kind regards
Your project now all done, based on discrete collected data,
collected data that you will have to smooth [not offered].
Smoothing is a large Engineering tool box !
I hope to be able to continue alone.
Let's see the continued adventure.
Cheers ... Jean
Maths Tangent Data Set.sm (60 КиБ) скачан 80 раз(а).
1 пользователям понравился этот пост
sergio 07.12.2019 11:50:00
#17 Опубликовано: 19.09.2024 22:40:49
Hello Alvaro, Is graphing a tangent line as exhibited in "curature3.sm" only available for a plot/function in parametric form, i.e. is this available for a cartesian plot/function?
I welcome your review and look forward to your reply.
Sincerely,
Norm
I welcome your review and look forward to your reply.
Sincerely,
Norm
#18 Опубликовано: 20.09.2024 07:35:36
Hi Norm. You can parametrize f(x) as {x(t)=t, y(t)=f(t)} and substitute in the formulas x'(t)=1, x''(t)=0, x(t) -> x and y(t) -> y(x).
curvatura3 - Cartesian.sm (40 КиБ) скачан 72 раз(а).
Best regards.
Alvaro.
curvatura3 - Cartesian.sm (40 КиБ) скачан 72 раз(а).
Best regards.
Alvaro.
1 пользователям понравился этот пост
sergio 21.09.2024 18:01:00
#19 Опубликовано: 20.09.2024 23:00:58
Thanks Alvaro! As always, great examples to work with!
Sincerely,
Norm
Sincerely,
Norm
1 страниц (19 вхождений)
-
 Новые сообщения
Новые сообщения
-
 Нет новых сообщений
Нет новых сообщений
