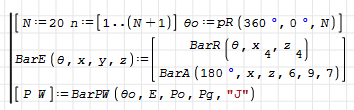x1^2+x2^2-x3^2=0;
(x1-1)^4+x2^4+(x3-2)^4-81=0;
x3 - 3*tan(0.4*x2)=0;



mod edit: please do not use non-descriptive links, use the proper attachment tools

Wrote

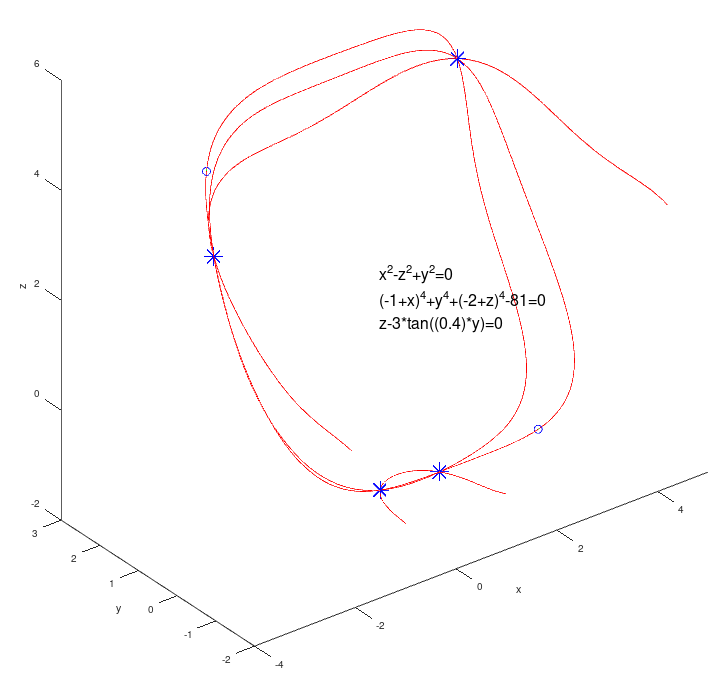
x1^2+x2^2-x3^2=0;
(x1-1)^4+x2^4+(x3-2)^4-81=0;
x3 - 3*tan(0.4*x2)=0;

Solutions to check out:
0.591395 -0.801312 -0.995916
-0.555082 -0.759905 -0.941049
-1.898741 1.789592 2.609187
3.362054 2.347994 4.100791

Some initial points:
2.598017 -0.736709 -0.953833
-1.826666 2.073210 4.007231
1.106031 -2.246909 -0.936232

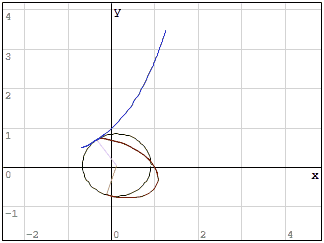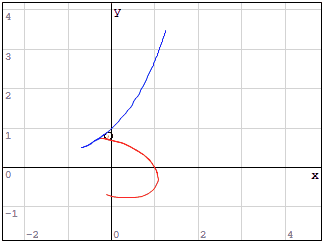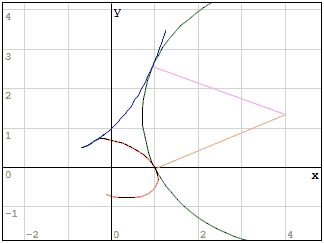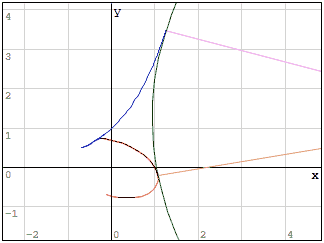
In the figure, the solutions are shown with an asterisk, the red curves are obtained when different initial conditions are given.

Wrote

Some initial points:
2.598017 -0.736709 -0.953833
-1.826666 2.073210 4.007231
1.106031 -2.246909 -0.936232

Зачем столько точек... Возьми (1,1,1) и по обе стороны от неё сразу найдёшь все решения.

Wrote

Wrote

Some initial points:
2.598017 -0.736709 -0.953833
-1.826666 2.073210 4.007231
1.106031 -2.246909 -0.936232

Зачем столько точек... Возьми (1,1,1) и по обе стороны от неё сразу найдёшь все решения.

Погрешность старался, чтобы поменьше получилась.
У тебя какая погрешность получилась при (1,1,1)?

Wrote

Погрешность старался, чтобы поменьше получилась.
У тебя какая погрешность получилась при (1,1,1)?

По корню квадратному из суммы квадратов невязок для каждой точки в среднем 6 нулей после запятой. Но, не забудь, Метод же не предназначен для высокой точности, потому что это численное решение ОДУ. Мы именно локализуем решения для последующего уточнения в случае необходимости. Поскольку я пользуюсь алгоритмами Maple, то часто бывает, что дальнейшего уточнения не требуется.
Посмотри статью Баранова, она в списке литературы Анатолия Владимировича

А. В. Баранов, “Об одном методе вычисления комплексных корней системы нелинейных
уравнений”, Ж. вычисл. матем. и матем. физ., 12:1 (1972), 199–203,.


Статья легко гуглится. В этой публикации, на мой взгляд, практически вся теория Метода.

Wrote

По корню квадратному из суммы квадратов невязок для каждой точки в среднем 6 нулей после запятой. Но, не забудь, Метод же не предназначен для высокой точности, потому что это численное решение ОДУ. Мы именно локализуем решения для последующего уточнения в случае необходимости. Поскольку я пользуюсь алгоритмами Maple, то часто бывает, что дальнейшего уточнения не требуется.
Посмотри статью Баранова, она в списке литературы Анатолия Владимировича

А. В. Баранов, “Об одном методе вычисления комплексных корней системы нелинейных
уравнений”, Ж. вычисл. матем. и матем. физ., 12:1 (1972), 199–203,.


Статья легко гуглится. В этой публикации, на мой взгляд, практически вся теория Метода.

У меня почему-то для одного из корней при единичках получилась относительно высокая погрешность, поэтому беру случайные значения и смотрю на погрешность. Но все равно не любое значение начальной точки дает все корни, многие точки быстро в бесконечность уходят.
Насколько я тебя понял есть методы, которые позволяют уточнять приближенное значение, но в практике они не используются.

grelkin2, приходи на киберфорум, там тоже есть такая тема, или просто в новою тему про конкретное уравнение. Хорошо?
Мне здесь очень неудобно: и пакета не знаю, и форум нерусский, и захожу по настроению... Заодно ваш SMath прорекламируешь.
Тамошнее имя у меня one man.

Wrote

grelkin2, приходи на киберфорум, там тоже есть такая тема, или просто в новою тему про конкретное уравнение. Хорошо?
Мне здесь очень неудобно: и пакета не знаю, и форум нерусский, и захожу по настроению... Заодно ваш SMath прорекламируешь.
Тамошнее имя у меня one man.

Я зарегался на mapleprimes, потихоньку смотрю и думаю, что написать в твои темы. Вроде там прилично. Я не знаток smath, использую для понимания алгоритмов в большей мере.
Насчет русских форумов у меня предубеждение. Обычно там или психи, или идиоты, или с личностными проблемами, если без модерации. Модерация нормальная или ты модератор?

grelkin2, там нормальная модерация, ну, со своей спецификой, конечно, но терпимая. Потом, разнообразие направлений. Там я никто, даже нарушитель, но тему под Метод выделили и терпят. C MaplePrimes какие для меня проблемы: во-первых, язык общения, во-вторых, сверх высокий профессиональный уровень большинства участников, в-третьих, мой сильно любительский Maple. Они, конечно, пытались и продолжают пытаться помочь... Но я же ничем, кроме Метода не интересуюсь, да и не знаю ничего за его рамками, а на наших форумах народ хоть и сильно тупее, и совсем недружелюбен, мягко говоря, но шанс пробить очередную публикацию есть. Иногда заходит публика с реальными вопросами и, случается, находят решение. Так появились аж три публикации, правда, было это ещё на сайте экспоненты.
(Твой сайт всегда недоступен.)

Wrote

grelkin2, там нормальная модерация, ну, со своей спецификой, конечно, но терпимая. Потом, разнообразие направлений. Там я никто, даже нарушитель, но тему под Метод выделили и терпят. C MaplePrimes какие для меня проблемы: во-первых, язык общения, во-вторых, сверх высокий профессиональный уровень большинства участников, в-третьих, мой сильно любительский Maple. Они, конечно, пытались и продолжают пытаться помочь... Но я же ничем, кроме Метода не интересуюсь, да и не знаю ничего за его рамками, а на наших форумах народ хоть и сильно тупее, и совсем недружелюбен, мягко говоря, но шанс пробить очередную публикацию есть. Иногда заходит публика с реальными вопросами и, случается, находят решение. Так появились аж три публикации, правда, было это ещё на сайте экспоненты.
(Твой сайт всегда недоступен.)

Ответил в лс.

On how to obtain equations of circles inscribed between smooth curves. The Draghilev method is used.
Topic on the MaplePrimes forum.

Интересная задача. Как спроектировать стол на шагающих ножках, чтобы поверхность стола оставалась горизонтальной.



Links:

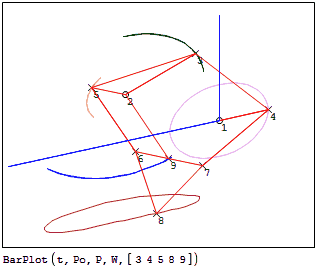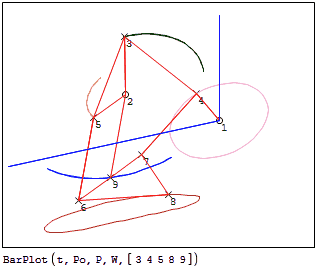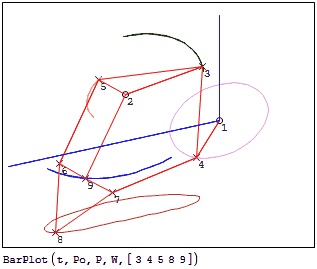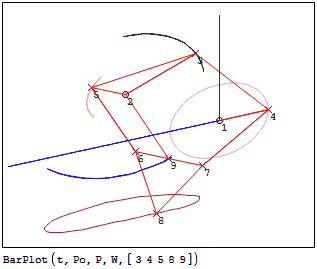
1.Carpentopod: A walking table project

Hi Viacheslav. You can try here the linkage bars system in general, and the Jansen's linkage in particular:

[albumimg]1679[/albumimg]

This is an approach to the carpentopod linkage, taking two fixed points. I guess that maybe it must have only one fixed point, BTW, it seems to move the table, although things on the table will probably fall off if the coefficient of friction is not high enough. So, take this just as a case study.



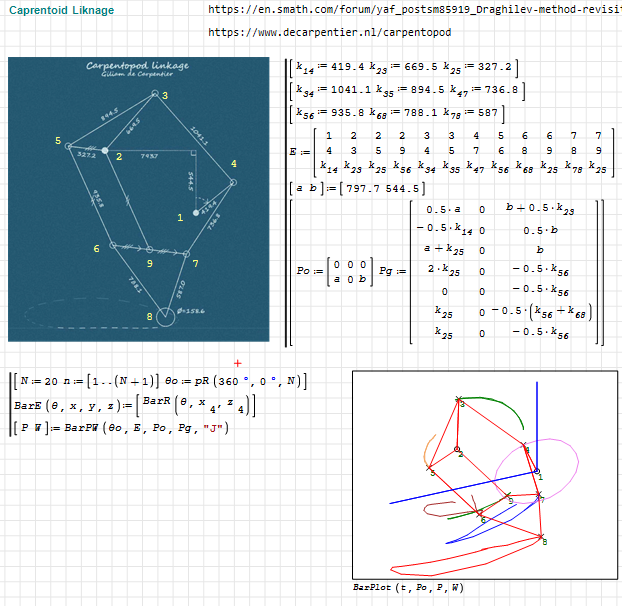
LinkageBars-carpentopod.pdf (601 КиБ) скачан 52 раз(а).

LinkageBars-carpentopod.sm (704 КиБ) скачан 50 раз(а).

Best regards.
Alvaro.

Adding the condition that points 6,9,7 are collinear, we have a stable solution.





Best regards.
Alvaro.

Wrote

On how to obtain equations of circles inscribed between smooth curves. The Draghilev method is used.
Topic on the MaplePrimes forum.

In SMath:

Inscribed Circles - Dragilev Method.sm (22 КиБ) скачан 59 раз(а).

Inscribed Circles - Dragilev Method.pdf (89 КиБ) скачан 60 раз(а).



Best regards.
Alvaro.

Не могу прикреить файлы. Помогите
Cann't attached files. Help

Wrote

Не могу прикреить файлы. Помогите
Cann't attached files. Help

There is a bug in the forum attachment dialog.

[RUS]Движение овала без поворота и без проскальзывания[/RUS]
[ENG]Movement of the oval without turning and without slipping[/ENG]

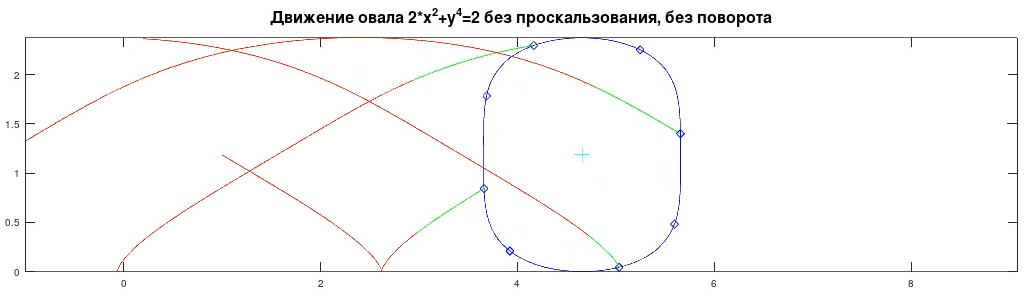
olv.mov (419 КиБ) скачан 47 раз(а).
[RUS]Движение овала с поворотом и без проскальзывания[/RUS]
[ENG]Movement of the oval with turning and without slipping[/ENG]

olv1.mov (519 КиБ) скачан 48 раз(а).
[RUS]Точки фигуры получаем хотя бы методом Драгилева. Меняем правую часть, чтобы складывалось движение по кривой и движение центра в случае, когда поворота нет. Когда поворот двигаем центра и вращаем точки по окружностям. Незабываем в этом случае вычесть минимальное значение, чтобы овал "катился".[/RUS]
[ENG]The points of the figure are obtained at least by Draghilev's method. We change the right part to add up the movement along the curve and the movement of the center when there is no rotation. When there is a rotation, we move the center and rotate the points on the circles. Remember to subtract the minimum value in this case, so that the oval “rolls”.[/ENG]

Wrote

... [RUS]Движение овала с поворотом и без проскальзывания[/RUS]
[ENG]Movement of the oval with turning and without slipping[/ENG] ...

This case, in SMath.

Rolling Oval - Dragilev Method.sm (14 КиБ) скачан 66 раз(а).



Best regards.
Alvaro.

Wrote

This case, in SMath.



Best regards.
Alvaro.

Very good, but there are some minor drawbacks. In linux smath does not work very well. I have all calculations going on the right side of de system. I calculate the coordinates of the tangent point and respectively the rotation speed of the oval. At the tangent point the velocity is zero and a tick icon is observed.