Wrote

Hi Jean. Try this, in the last portable version (0.99.6839.38235):

Syntax is incorrect ... 6839 is totally not compatible 6179.
Hard to explain: first time Draghilev was offered it did open 5346 !

About the coding below, is it the latest way to code 6839 ?
What kind of coding is that ? Remember the Alex project
I re-coded it all and worked fine.

Cheers ... Jean

Wrote

Razonar, you are not talking about the method of Draghilev, but about your understanding of it. This is not the same thing.

Sure. Doesn't same thing apply to you too?

Wrote

... And: what is the relation to the essence have the lengths of the arcs, parametrization...?

A lot. For instance, from the paper that you give as reference ( https://vk.com/doc242471809_437831729 ) can read:


...


...
"From the course of mathematical analysis, we know that the length of the arc does not depend on the choice of the parameter t, and it increases with t. The value t = 0 corresponds to the selected starting point, from which the curve will be constructed in both directions, in the “positive” direction the integration step will be positive, and in the “negative” direction - negative. To solve (2a), we can apply the standard algorithm for the numerical solution of the Cauchy problem to construct the curve (1)."

...
"We construct the curve (1), assuming that the length of the arc of the curve itself is the independent variable. The coordinates of the points of the curve will be obtained as a solution to the Cauchy problem for a system of ordinary differential equations, the initial data for which will be the coordinates of the previously known point belonging to this curve"

But the final parametrization isn't along the arc length.

Best regards.
Alvaro.

Wrote

Wrote

Hi Jean. Try this, in the last portable version (0.99.6839.38235):

About the coding below, is it the latest way to code 6839 ?
What kind of coding is that ?

Hi Jean. What you see is the unicode code for some ornaments. I use them because I don't like the use of x#, y# ... etc for each variable in the definition and body of the SMath procedures.



Maybe you don't have the unicode version of Courier New font.

Best regards.
Alvaro.

Wrote

Maybe you don't have the unicode version of Courier New font.

Special characters mode is available since Version 0.99.6617, hence can't be rendered correctly in Jean's 0.98.6179 (no matter what fonts he has)

Please note that decorations aren't really needed since 0.98.6325 when Clear() was made built-in and that is enough to isolate line() procedures from external variables (useful in Jean's 0.98.6179, though)

Wrote

Please note that decorations aren't really needed since 0.98.6325 when Clear() was made built-in and that is enough to isolate line() procedures from external variables (useful in Jean's 0.98.6179, though)

Hi Davide. Thanks for confirm that, I still using both.

Best regards.
Alvaro.

Wrote

...
But the final parametrization isn't along the arc length.
...

What is the meaning of your messages? Using the arc length as an independent variable is a well-known technique and is not directly related to the Draghilev method, but can be used in the implementation of the method. For example, I widely use this technique. This is achieved by simple normalization of the variable of integration by the magnitude (dx^2 + dy^2 + dz^2)^0.5, in the case of 3d.

Yes, I hope you understand that the curve itself is always unambiguous?

Wrote

Wrote

...
But the final parametrization isn't along the arc length.
...

What is the meaning of your messages? Using the arc length as an independent variable is a well-known technique and is not directly related to the Draghilev method, but can be used in the implementation of the method. For example, I widely use this technique. This is achieved by simple normalization of the variable of integration by the magnitude (dx^2 + dy^2 + dz^2)^0.5, in the case of 3d.

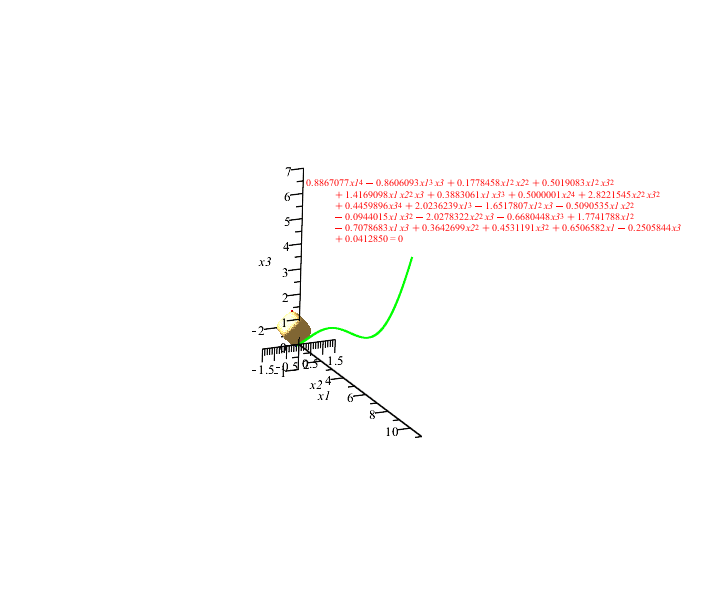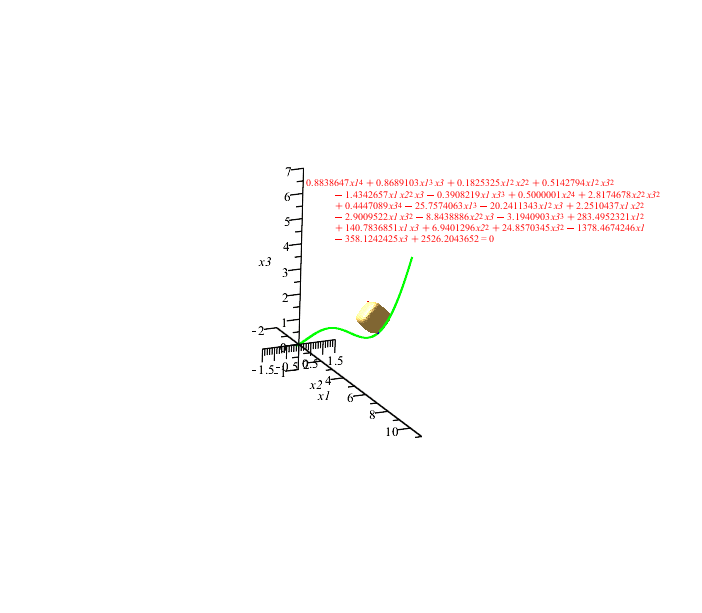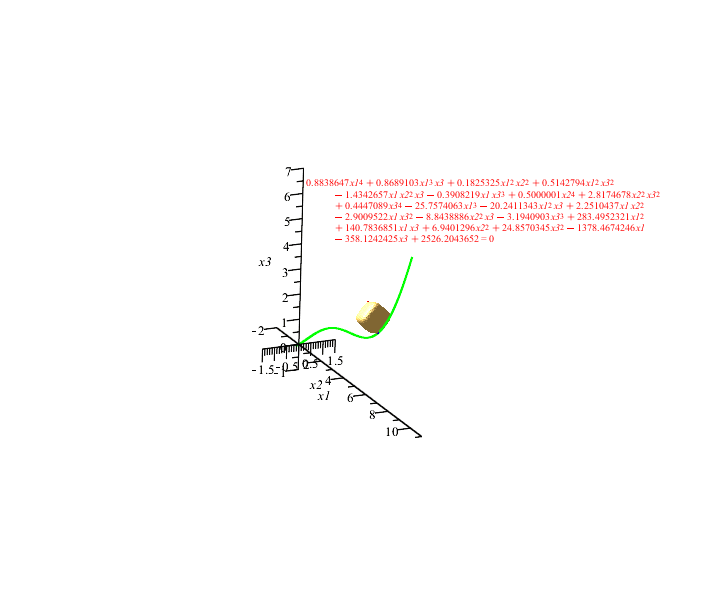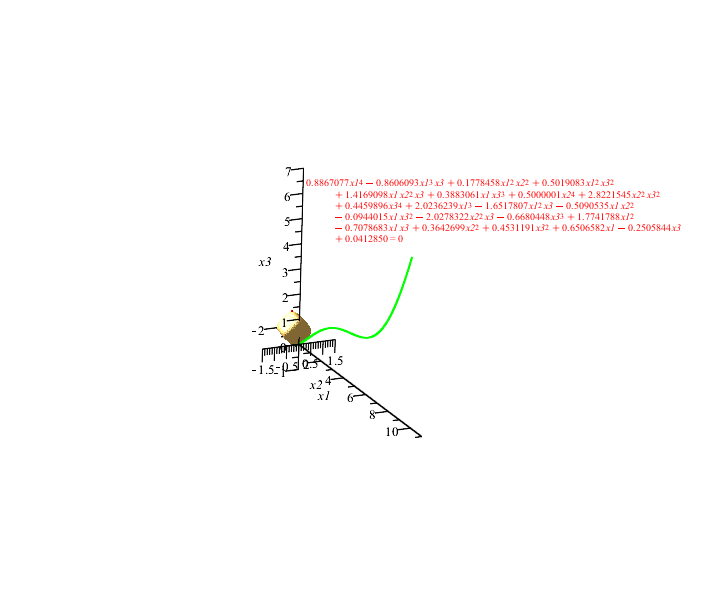
The referenced paper talks about parametrizing along the arc length, but the results that I see aren't like that. Please check the green marked areas:

dm_not_s.sm (91 КиБ) скачан 73 раз(а).
dm_not_s.pdf (223 КиБ) скачан 81 раз(а).

Wrote

Yes, I hope you understand that the curve itself is always unambiguous?

You don't parametrize curves, you parametrize paths. For disambiguation, after you found a parametrization for some path, you must to provide the parameter range where you want to represent the curve. As the classic example, you have the circumference . It's your "curve" just only one "circumference" or could be it a circumference and a half? Curves can intercept itself as many times as they want. How many times do you want or need to cover the circumference? Just only one or several times? You answer those questions choosing the adequate parameter range.

Certainly, this is my last answer to you.

Alvaro.

Wrote

I hope you understand that the curve itself is always unambiguous?

Unambiguous curves are baby stuff.
In Engineering, we rarely have have such ideal maths formulae whereas the project
is generally a suite to data sets best approximated from optimizing model.
On the other hand, practical arc length depends upon built-in numerical integrator(s).
In the attached, observe the native Smath Simpson vs Smath-Romberg.
On the other end the contract may require double check from independent methods.
The attached includes Legendre [one of the most used from reference]

Cheers ... Jean

Integrate Wisely [Arc Lagrange].sm (46 КиБ) скачан 83 раз(а).

Razonar.

"We construct the curve (1), предположив=suggesting (not assuming) that the length of the arc of the curve itself is the independent variable. The coordinates of the points of the curve will be obtained as a solution to the Cauchy problem for a system of ordinary differential equations, the initial data for which will be the coordinates of the previously known point belonging to this curve"

By the way, where did you find the "parameterization" in the description?
“But the final parametrization isn't along the arc length.”

I do not have and do not use SMath.
Both the circumference and the length of any closed smooth curve can be constructed either by any part, or by any repetitions, giving the coordinates of points a unique dependence on the arc length. The coordinates of the points are functions of the arc length.

Guys, everything works by fundamentals of elementary mathematics and works in areas that were very complex before the advent of the Draghilev method.
Good luck to you in understanding and mastering the Method.

Wrote

I do not have and do not use SMath.

It seems to me that SMath does not yet has the capabilities, such as Maple, to execute some examples.:d

For example, Method Draghilev, however:
[albumimg]1591[/albumimg] [albumimg]1592[/albumimg]

Wrote

...
If you find some volunteers to code Tom G. Mathcad contour ... please feel free.
...

Hi Jean. Problem for code in SMath this procedure it's about that NaN is unavaible in SMath. Here you can see what happens without NaN, and a workaround of that:

https://en.smath.info/forum/yaf_postst12539_Implicit-Plot.aspx



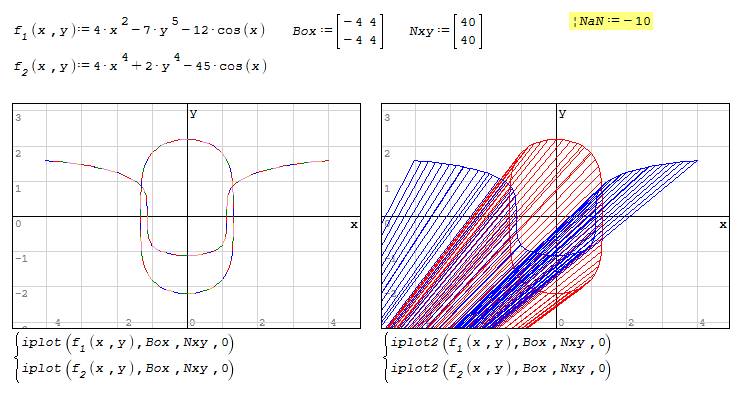
iplotq.sm (40 КиБ) скачан 120 раз(а).

The iplot routine is from uni works in mathdcad.

Best regards.
Alvaro.

Dragilev method for equations with a parameter.Equations borrowed from Jean Giraud .



JeanContour1.sm (11 КиБ) скачан 81 раз(а).
Jean.sm (11 КиБ) скачан 84 раз(а).

Wrote

Dragilev method for equations with a parameter.Equations borrowed from Jean Giraud .

Thanks Ber7 ... Electron function works fine.
Loop function fails, Maple SS 6179 seems in cause [RootOf].
Tried to doctor, not to avail , Ah !

Jean

... doctored: few cut/paste has like re-installed the codes,
Can't get the complete loop as yours, but pleased with other contours.

Thanks again ... gorgeous Draghilev/Ber7

Jean, try without a maple.
Jeansolve.sm (11 КиБ) скачан 79 раз(а).

Wrote

Jean, try without a maple.

It works fine but can't nicely complete the 0 level loop.
It can be done otherwise for the interest of exporting.
This LaceLoop origin from Mathsoft Collaboratory... why ?
Mathcad 11 contour plot does nothing except absolute scrap.
So intriguing, that Tom G. made his own superb contour program.

Jean

Draghilev's Contour_2 Ber7 [Loop NO maple].sm (85 КиБ) скачан 81 раз(а).
Draghilev's Contour_2 Ber7 [Loop Reconciliation].sm (86 КиБ) скачан 77 раз(а).

Point chart. You can see that the distance between the points is the same(Version 0.99.6839)

Version 0.99.6839.sm (11 КиБ) скачан 76 раз(а).

Thanks Ber7 for the Draghilev parametric method.
I'm in peace with myself from the attached reconciliation.
Bigger image in the document.

Jean



Draghilev's Contour_2 Ber7 [Loop Reconciliation] Copy.sm (152 КиБ) скачан 80 раз(а).

The parameterization by Draghilev method.The starting point is taken near the bifurcation point (0,0).

ContourTifoleum.sm (16 КиБ) скачан 80 раз(а).

Wrote

Point chart. You can see that the distance between the points is the same(Version 0.99.6839)

Hi Ber. Great discover! If you can translate that as a general result, this is, you can relate the distance between points and the parameter, it could be an important theoretical result, given access to parametrize the curve between two given points. The starting point (x0,y0) or (x0,y0,z0) with t=0, and with that relation you can know previously for which t=t1 you touch another curve point (x1,y1). Further you can evaluate with the parametric formulas areas (double or triple integrals), path integrals, fluxes integrals, frenet vectors, and others with parametric formulations, which are more stable and accurate numerically than those from cartesian forms. Also, maybe you can investigate the symbolics results, using dsolve from maple or maxima instead the numeric rkfixed solutions for inspect how the parametrization is constructed.

I see that that you divide by the jacobian determinant, which I guess result in the parametrization by the arc lenght curve. As a minor observation you can improve that, avoiding transposition under the square root, accessing jacobian elements by the SMath el(n) with only one argument for matrices.

Best regards.
Alvaro.