1 страниц (16 вхождений)
Решение СНУ - Сообщения
#1 Опубликовано: 23.10.2010 06:51:08
Одномерный случай.
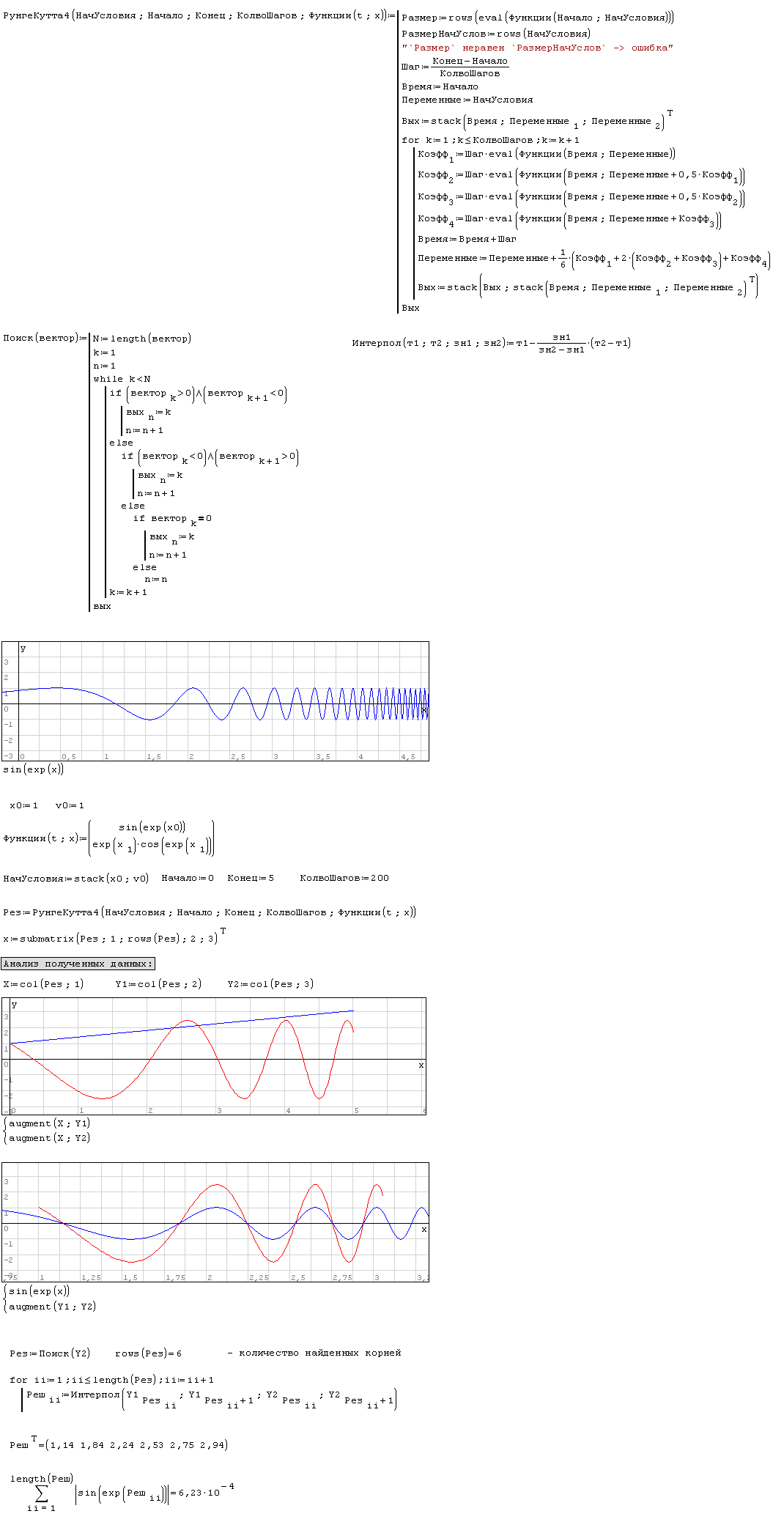
Уравнение: [MATH]sin(exp(x))=0[/MATH]
Документ: Решение СНУ 2.sm
Пояснения:
Это тривиальный случай. Более понятным будут большие размерности.
Мы заменяем исходное уравнение немножко другим, добавляя одну переменную v.
Смысл замены в том, чтобы новая кривая спокойно проходила нули. Новое уравнение построено таким образом, что содержит все корни старого уравнения.
Находим дифурчик, который соответствует новой кривой. С помощью решателя диффура восстанавливаем интегральную кривую, начиная с условия v=1. Мы должны идти вдоль начального уравнения. Конкретно в этом случае можно взять любое значение x, чтобы "сесть" на кривую. В задачах с большей размерностью проще всего взять одно известное решение системы. Новая кривая, выходя из v=1 проходит все нули исходного уравнения. Мы отбираем те, где знак v изменился. Можно, конечно и по самой функции так пройтись, но смысл будет понятен позже, когда я покажу работу алгоритма в трёхмерном пространстве.
Уравнение: [MATH]sin(exp(x))=0[/MATH]
Документ: Решение СНУ 2.sm
Пояснения:
Это тривиальный случай. Более понятным будут большие размерности.
Мы заменяем исходное уравнение немножко другим, добавляя одну переменную v.
Смысл замены в том, чтобы новая кривая спокойно проходила нули. Новое уравнение построено таким образом, что содержит все корни старого уравнения.
Находим дифурчик, который соответствует новой кривой. С помощью решателя диффура восстанавливаем интегральную кривую, начиная с условия v=1. Мы должны идти вдоль начального уравнения. Конкретно в этом случае можно взять любое значение x, чтобы "сесть" на кривую. В задачах с большей размерностью проще всего взять одно известное решение системы. Новая кривая, выходя из v=1 проходит все нули исходного уравнения. Мы отбираем те, где знак v изменился. Можно, конечно и по самой функции так пройтись, но смысл будет понятен позже, когда я покажу работу алгоритма в трёхмерном пространстве.
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:51:00
#2 Опубликовано: 23.10.2010 08:27:41
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:51:00
#3 Опубликовано: 23.10.2010 12:58:52
Двумерный случай.
Система нелинейных уравнений: [MATH]sys(4*(y-1)^2+(x-1)^2-1≡0;y-x*sin(25*x)≡0;2;1)[/MATH]

Документ: Решение СНУ 4.sm
Пояснения: Начальная точка (0,4; 0,58) - не лежит ни на одной из кривых, поэтому интегральная кривая будет являться по виду чем-то средним между обеими кривыми в зависимости от начальной точки. Если взять точку на эллипсе, то проекция 3D кривой будет эллипсом, если взять точку на синусоиде, то и проекция кривой будет повторять синусоиду. Т.о. мы выбираем по какой кривой двигаться.
Тем не менее, видно, что мы нашли все 16 решений системы, двигаясь вдоль одного параметра.
Система нелинейных уравнений: [MATH]sys(4*(y-1)^2+(x-1)^2-1≡0;y-x*sin(25*x)≡0;2;1)[/MATH]
Документ: Решение СНУ 4.sm
Пояснения: Начальная точка (0,4; 0,58) - не лежит ни на одной из кривых, поэтому интегральная кривая будет являться по виду чем-то средним между обеими кривыми в зависимости от начальной точки. Если взять точку на эллипсе, то проекция 3D кривой будет эллипсом, если взять точку на синусоиде, то и проекция кривой будет повторять синусоиду. Т.о. мы выбираем по какой кривой двигаться.
Тем не менее, видно, что мы нашли все 16 решений системы, двигаясь вдоль одного параметра.
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:51:00
#4 Опубликовано: 23.10.2010 14:31:04
Система диффуров для двумерного случая получается путём векторного перемножения нормалей поверхностей.
Эта система описывает линию пересечения поверхностей в 3D. Если выбрать на этой линии точку и построить вектора нормалей к обеим поверхностям, а потом их векторно перемножить, то результирующий вектор будет направлен вдоль касательной к линии пересечения. Решение же диффура методом Рунге-Кутта - есть восстановление линии пересечения поверхностей, т.е. построение интегральной кривой. Ясно, что эта кривая проходит через все решения системы (односвязные). Она как ниточка с иголкой протыкает пространство на размерность меньше в точках решения.

Нули в векторе - это специальный приём. Чтобы не пересчитывать вектор D(t,x) для каждой начальной точки, эти точки вводятся в сам диффур в качестве неиспользуемых переменных (0 - это константа при интегрировании). Поэтому в самом решателе диффура можно ссылаться на эти константы.
Эта система описывает линию пересечения поверхностей в 3D. Если выбрать на этой линии точку и построить вектора нормалей к обеим поверхностям, а потом их векторно перемножить, то результирующий вектор будет направлен вдоль касательной к линии пересечения. Решение же диффура методом Рунге-Кутта - есть восстановление линии пересечения поверхностей, т.е. построение интегральной кривой. Ясно, что эта кривая проходит через все решения системы (односвязные). Она как ниточка с иголкой протыкает пространство на размерность меньше в точках решения.
Нули в векторе - это специальный приём. Чтобы не пересчитывать вектор D(t,x) для каждой начальной точки, эти точки вводятся в сам диффур в качестве неиспользуемых переменных (0 - это константа при интегрировании). Поэтому в самом решателе диффура можно ссылаться на эти константы.
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:52:00
#5 Опубликовано: 26.10.2010 11:18:38
Двумерный случай (с Лемнискатой Бурнулли).
Система нелинейных уравнений:[MATH]sys((2/3*y)^2+(4*x)^2-1≡0;-x^2+y^2-(x^2+y^2)^2≡0;2;1)[/MATH]

Документ: Решение СНУ 5.sm
П.С. Наверное это можно сделать немного проще, учитывая наличие явной формулы для Лемнискаты, но не уверен. Вообще говоря, уже давно пора не ограничивать себя только численными методами, как это делают в дискретной математике. Современная вычислительная техника и технологии программирования шагнули далеко вперёд и что 50 лет назад считалось фантастикой, сегодня обыденность дня.
Система нелинейных уравнений:[MATH]sys((2/3*y)^2+(4*x)^2-1≡0;-x^2+y^2-(x^2+y^2)^2≡0;2;1)[/MATH]
Документ: Решение СНУ 5.sm
П.С. Наверное это можно сделать немного проще, учитывая наличие явной формулы для Лемнискаты, но не уверен. Вообще говоря, уже давно пора не ограничивать себя только численными методами, как это делают в дискретной математике. Современная вычислительная техника и технологии программирования шагнули далеко вперёд и что 50 лет назад считалось фантастикой, сегодня обыденность дня.
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:52:00
#6 Опубликовано: 26.10.2010 14:33:37
См. похожую задачу
http://communities.ptc.com/videos/1472
http://communities.ptc.com/videos/1472
#7 Опубликовано: 27.10.2010 12:38:14
Да, кстати, по поводу этого метода нахождения решений. Называется он - метод Драгилева. Научил меня им пользоваться Алексей (Иванов А. Б.), который тут был не понят  Судя по словам Алексея Борисовича, метод является усовершенствованием метода продолжения по параметру. Нашёл тут книжку, где есть кое-что как раз в тему этого метода:
Судя по словам Алексея Борисовича, метод является усовершенствованием метода продолжения по параметру. Нашёл тут книжку, где есть кое-что как раз в тему этого метода:
В. И. Шалашилин, Е. Б. Кузнецов, Метод продолжения решения по параметру и наилучшая параметризация в прикладной математике и механике, Эдиториал УРСС, Москва, 1999 г, с. 222.
Ссылка на диссертацию по этой работе одного из воспитанников автора (Е. Б. Кузнецов): Параметризация вычислительного процесса в задачах математического моделирования, Красников С. Д., М., 2008 г. (05.13.18)
Книжка есть в электронном виде в сети (djvu). Там есть начальная теория. Жаль я не математик и в моей инженерной практике такие знания не нужны, хотя аспирантуру начинал по этой же специальности (05.13.18). Может быть мне кто-нить растолкует чем отличается подход в диссертации от подхода в методе Драгилева и какие цели и там, и там преследуются.
В. И. Шалашилин, Е. Б. Кузнецов, Метод продолжения решения по параметру и наилучшая параметризация в прикладной математике и механике, Эдиториал УРСС, Москва, 1999 г, с. 222.
Ссылка на диссертацию по этой работе одного из воспитанников автора (Е. Б. Кузнецов): Параметризация вычислительного процесса в задачах математического моделирования, Красников С. Д., М., 2008 г. (05.13.18)
Книжка есть в электронном виде в сети (djvu). Там есть начальная теория. Жаль я не математик и в моей инженерной практике такие знания не нужны, хотя аспирантуру начинал по этой же специальности (05.13.18). Может быть мне кто-нить растолкует чем отличается подход в диссертации от подхода в методе Драгилева и какие цели и там, и там преследуются.
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:52:00
#8 Опубликовано: 27.10.2010 15:21:03
Двумерный случай (экстремумы функции Химмельблау). Посмотрим на влияние выбора начальной точки при восстановлении интегральной кривой.
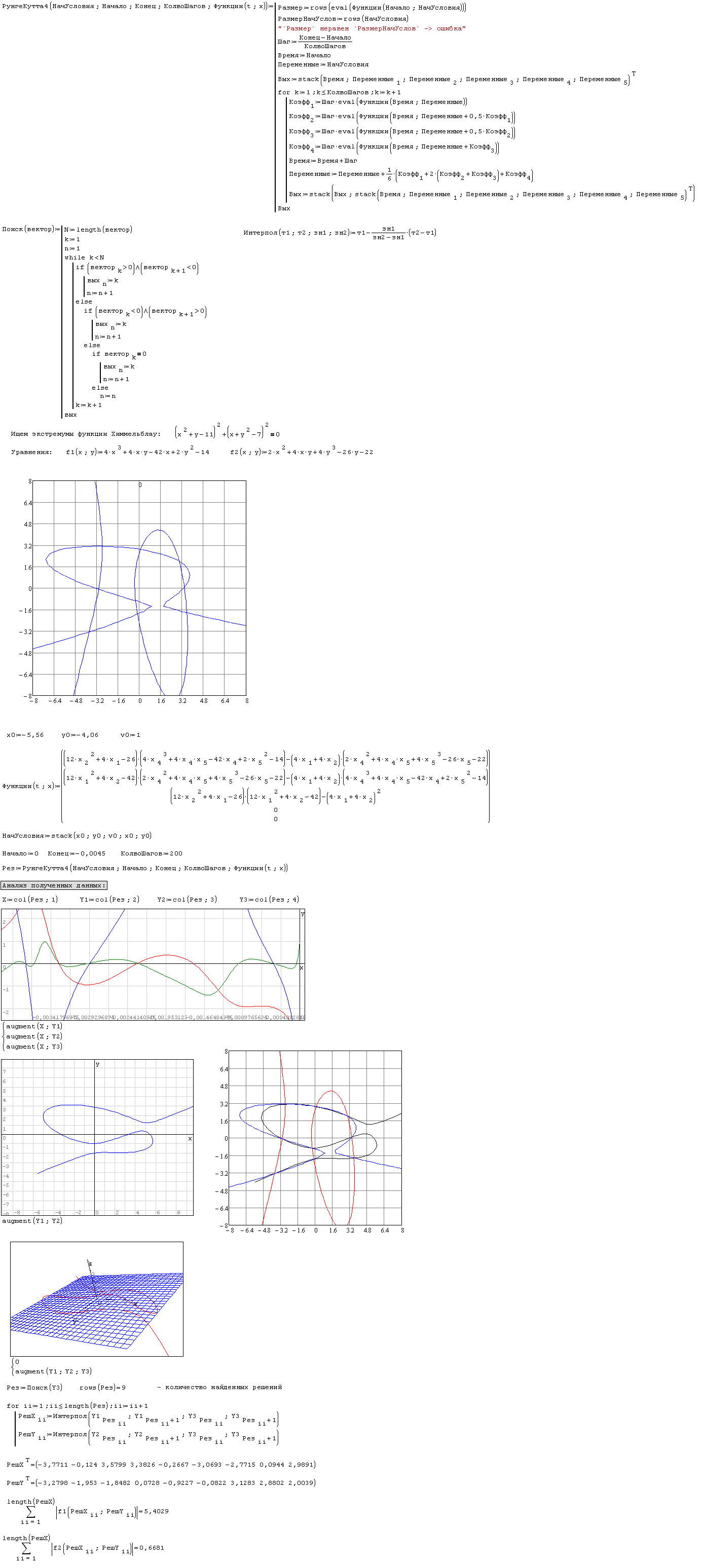
Задачка: найти все точки экстремума функции Химмельблау [MATH]f(x;y)←(x^2+y-11)^2+(x+y^2-7)^2[/MATH]

Вариант 1. Точка (-5,56; 4,06) - эта точка выбиралась графически, как лежащая на втором уравнении. Было выбрано именно второе уравнение, т.к. оно односвязно и проходит все точки экстремума - нули производных.
Документ: Решение СНУ 6_1.sm
Задачка: найти все точки экстремума функции Химмельблау [MATH]f(x;y)←(x^2+y-11)^2+(x+y^2-7)^2[/MATH]

Вариант 1. Точка (-5,56; 4,06) - эта точка выбиралась графически, как лежащая на втором уравнении. Было выбрано именно второе уравнение, т.к. оно односвязно и проходит все точки экстремума - нули производных.
Документ: Решение СНУ 6_1.sm
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:52:00
#9 Опубликовано: 27.10.2010 15:36:50
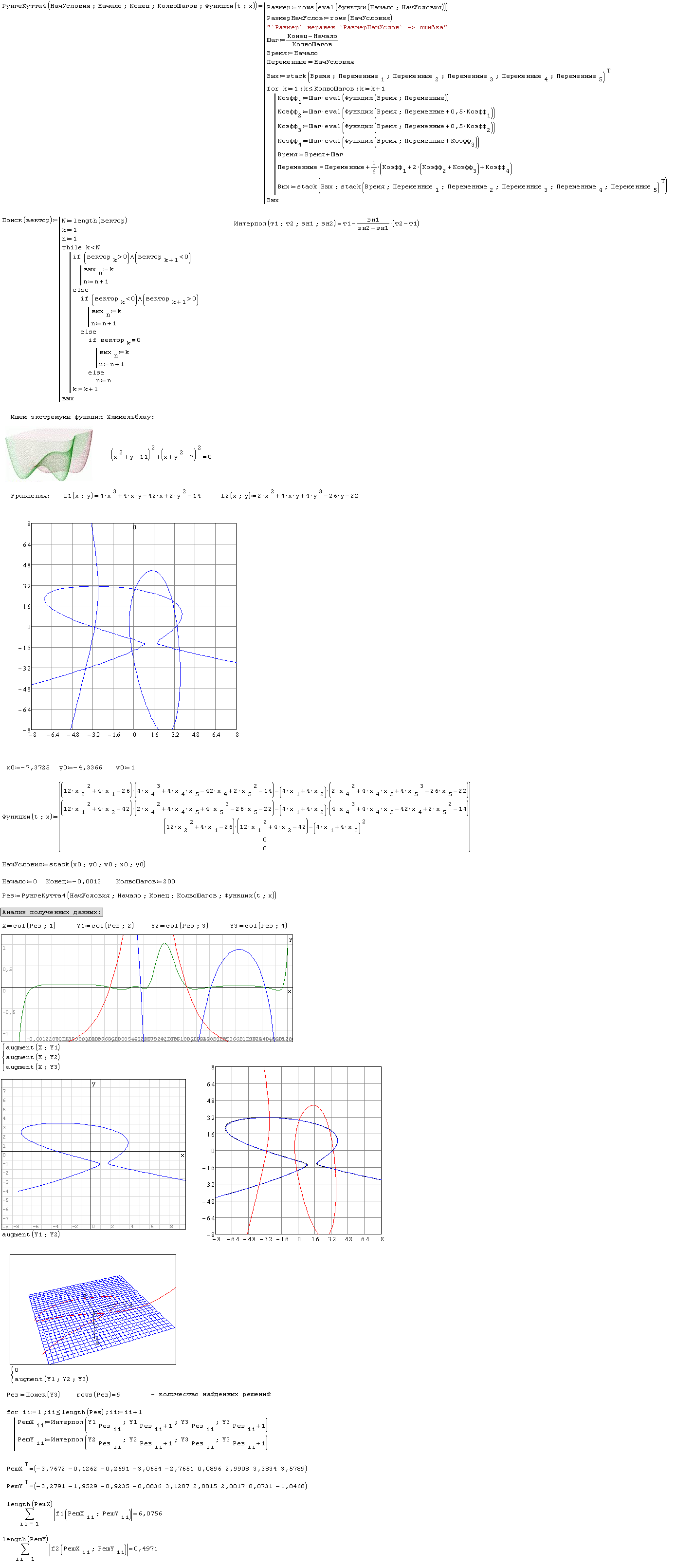
Задачка: найти все точки экстремума функции Химмельблау [MATH]f(x;y)←(x^2+y-11)^2+(x+y^2-7)^2[/MATH]
Вариант 2. Точка (-7.3725; -4.3366) На картинке я уравнение приравнял к нулю - это атавизм Нужно найти экстремумы.
Нужно найти экстремумы.
Документ: Решение СНУ 6_2.sm
Решение уже идёт конкретно вдоль второго уравнения, чтобы не сбиться с пути
Точность оставляет желать лучшего. Интересно было бы посмотреть на итерационные методы на этой же задачке.
Вариант 2. Точка (-7.3725; -4.3366) На картинке я уравнение приравнял к нулю - это атавизм
Документ: Решение СНУ 6_2.sm
Решение уже идёт конкретно вдоль второго уравнения, чтобы не сбиться с пути
Точность оставляет желать лучшего. Интересно было бы посмотреть на итерационные методы на этой же задачке.
Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:53:00
#10 Опубликовано: 30.10.2010 13:33:14
WroteДвумерный случай (с Лемнискатой Бурнулли).
Система нелинейных уравнений:[MATH]sys((2/3*y)^2+(4*x)^2-1≡0;-x^2+y^2-(x^2+y^2)^2≡0;2;1)[/MATH]
П.С. Наверное это можно сделать немного проще, учитывая наличие явной формулы для Лемнискаты, но не уверен. Вообще говоря, уже давно пора не ограничивать себя только численными методами, как это делают в дискретной математике. Современная вычислительная техника и технологии программирования шагнули далеко вперёд и что 50 лет назад считалось фантастикой, сегодня обыденность дня.
Известно, что пакет Математика 7 находит все корни алгебраических систем. Причём довольно шустро… При этом не доводилось слышать, что проблемы полного решения СНАУ уже не существует. Интересно узнать, а с помощью Вашего метода можно найти ВСЕ решения алгебраической системы уравнений?
#11 Опубликовано: 14.01.2012 21:45:32
Доброго времени суток!
уни, хотелось бы Вас поблагодарить за подробное иллюстрированное и концентрированное изложение метода Драгилева, описание которого приведено на "exponenta.ru". Но там несколько обширных тем, в которых я просто заблудился . Извините, тема еще актуальна? Хотелось бы задать несколько вопросов.
. Извините, тема еще актуальна? Хотелось бы задать несколько вопросов.
уни, хотелось бы Вас поблагодарить за подробное иллюстрированное и концентрированное изложение метода Драгилева, описание которого приведено на "exponenta.ru". Но там несколько обширных тем, в которых я просто заблудился
#12 Опубликовано: 15.01.2012 02:11:57
А Вы обратитесь там же с конкретным вопросом, и Вам, уверен, подробно ответят...
#13 Опубликовано: 15.01.2012 18:34:23
Спасибо!
У «экспоненты» есть одно свойство– необходимость подвешивать файлы вложений на внешние обменники. Через некоторое время такие файлы имеют свойство пропадать. И пароль там генерит сама система и я его постоянно забываю, тк редко пользуюсь .
.
Поэтому уж здесь, если не затруднит, то вот такие пока вопросы. Я не математик, поэтому извините, если что-то совсем коряво буду излагать, или очень очевидные вещи спрашивать.
Для определенности можно рассматривать плоскую задачу о пересечении двух кривых, заданных в неявном виде. Тут можно простое геометрическое толкование задачи придумать, что для понимания тоже неплохо.
1. Исходную систему уравнений в ряде случаев необходимо приводить к виду, когда
Число_ переменных =число_ уравнений + 1 (или я не прав?)
Существуют ли какие-либо алгоритмы или рекомендации по выполнению такого приведения? Или это больше искусство, и все зависит от конкретного случая?
2. Выбор начального условия. Получается, что первоначально нужно знать хотя бы одну точку пересечения. Есть ли алгоритмы поиска таких точек с использованием самого Метода?
У «экспоненты» есть одно свойство– необходимость подвешивать файлы вложений на внешние обменники. Через некоторое время такие файлы имеют свойство пропадать. И пароль там генерит сама система и я его постоянно забываю, тк редко пользуюсь
Поэтому уж здесь, если не затруднит, то вот такие пока вопросы. Я не математик, поэтому извините, если что-то совсем коряво буду излагать, или очень очевидные вещи спрашивать.
Для определенности можно рассматривать плоскую задачу о пересечении двух кривых, заданных в неявном виде. Тут можно простое геометрическое толкование задачи придумать, что для понимания тоже неплохо.
1. Исходную систему уравнений в ряде случаев необходимо приводить к виду, когда
Число_ переменных =число_ уравнений + 1 (или я не прав?)
Существуют ли какие-либо алгоритмы или рекомендации по выполнению такого приведения? Или это больше искусство, и все зависит от конкретного случая?
2. Выбор начального условия. Получается, что первоначально нужно знать хотя бы одну точку пересечения. Есть ли алгоритмы поиска таких точек с использованием самого Метода?
#14 Опубликовано: 06.10.2012 07:33:40
Я полностью автоматизировал работу алгоритма в SMath. Единственное пока неудобство - это необходимость внешнего плагина для его работы: MapleWrapper плагин.
Дело в том, что мне нужно особым образом вычислять Якобиан, а встроенная функция не достаточно ещё реализована. Поэтому приходится пользоваться услугами maple через вышеуказанный плагин.
Много примеров по работе с методом я выложил на параллельном английском форуме: Draghilev's method.
Ответы на последние вопросы:
1. Сейчас реализация метода самостоятельно делает все необходимые преобразования, поэтому можно не думать о ещё одной переменной, а просто задать систему.
2. Начальное условие не обязательно должно быть решением системы. Если обратиться к аналогии, то можно сказать так: для случая двух уравнений и двух переменных первоначальная точка должна быть решением одного из входящих в систему уравнений.
Что касается работы с функцией Draghilev(), то я остановлюсь попозже более подробно на тонких моментах настройки решателя, но это вовсе не исключает понимания хотя бы общих принципов теории. Я старался иллюстрировать примеры, поэтому советую начать именно с них и пройтись по каждому.
Дело в том, что мне нужно особым образом вычислять Якобиан, а встроенная функция не достаточно ещё реализована. Поэтому приходится пользоваться услугами maple через вышеуказанный плагин.
Много примеров по работе с методом я выложил на параллельном английском форуме: Draghilev's method.
Ответы на последние вопросы:
1. Сейчас реализация метода самостоятельно делает все необходимые преобразования, поэтому можно не думать о ещё одной переменной, а просто задать систему.
2. Начальное условие не обязательно должно быть решением системы. Если обратиться к аналогии, то можно сказать так: для случая двух уравнений и двух переменных первоначальная точка должна быть решением одного из входящих в систему уравнений.
Что касается работы с функцией Draghilev(), то я остановлюсь попозже более подробно на тонких моментах настройки решателя, но это вовсе не исключает понимания хотя бы общих принципов теории. Я старался иллюстрировать примеры, поэтому советую начать именно с них и пройтись по каждому.
Россия навсегда!
Вячеслав Мезенцев
#15 Опубликовано: 14.11.2013 18:06:36
Уважаемый Вячеслав,не могли бы показать Вы решение этого примера
методом Драгилева? Ваше решение послужит мне образцом для нахождения
координат звеньев других механизмов.
С уважением,Фридель.
maplePrimer1.sm (25,88 КиБ) скачан 1243 раз(а).
методом Драгилева? Ваше решение послужит мне образцом для нахождения
координат звеньев других механизмов.
С уважением,Фридель.
maplePrimer1.sm (25,88 КиБ) скачан 1243 раз(а).
Метод расчета рычажных механизмов :http://www.exponenta.ru/educat/systemat/selitskiy-ivanov/index.asp
#16 Опубликовано: 15.11.2013 13:49:31
Доброго Фридель.
При такой постановке задачи я не знаю как применить метод. В данном случае не хватает каких-то дополнительных условий. Решения могут быть закручены как по часовой стрелке, так и против часовой стрелки, а это неопределённость в постановке. Метод Драгилева ищет численные решения в строго определённых (аналитичных) системах. Ещё мне не совсем ясно на счёт того что задано и что нужно найти. Если начальные координаты отрезка заданы, то найти координаты второго конца можно и без метода Драгилева при помощи функций для решения систем нелинейных уравнений, которые есть в соотв-щем дополнении.
При такой постановке задачи я не знаю как применить метод. В данном случае не хватает каких-то дополнительных условий. Решения могут быть закручены как по часовой стрелке, так и против часовой стрелки, а это неопределённость в постановке. Метод Драгилева ищет численные решения в строго определённых (аналитичных) системах. Ещё мне не совсем ясно на счёт того что задано и что нужно найти. Если начальные координаты отрезка заданы, то найти координаты второго конца можно и без метода Драгилева при помощи функций для решения систем нелинейных уравнений, которые есть в соотв-щем дополнении.
Россия навсегда!
Вячеслав Мезенцев
1 страниц (16 вхождений)
- Новые сообщения
- Нет новых сообщений
