Just confusing it does not evaluate correct Φ(0)=0.5

Bug Heaviside.sm (10 КиБ) скачан 93 раз(а).

Wrote

Just confusing it does not evaluate correct Φ(0)=0.5

Hi Jean. Heaviside, and it's brother, Dirac, aren't functions, are distributions: https://en.wikipedia.org/wiki/Distribution_(mathematics)

Also can check this at: https://reference.wolfram.com/language/tutorial/GeneralizedFunctionsAndRelatedObjects.html

Distributions came from the develop of french mathematicians, as the limit of successions of functions. Because are not functions, they don't have the usual properties, and are a kind of extension of the concept of functions, but can't be handled without some precautions.

From Maple 5 help:

---

Description:
The Dirac and Heaviside functions are distributions. The Dirac(t) delta function is defined as zero everywhere except at t = 0 where it has a singularity. It also has the property that
Int(Dirac(t),t = -infinity..infinity) = 1
Derivatives of the Dirac function are denoted by the two-argument Dirac function. The first argument denotes the order of the derivative. For example, diff(Dirac(t), t$n) will be automatically simplified to Dirac(n, t) for any integer n.
The Heaviside(t) function is defined as zero for t < 0, 1 for t > 0 and is not defined at 0. It is related to the Dirac function by diff(Heaviside(t),t) = Dirac(t).
These functions are typically used in the context of integral transforms such as laplace(), mellin() or fourier() or the solving of differential equations. They are also used to represent piecewise continuous functions with conversion routines available.

---

So, value at 0 is undefined for Maple 5, but in newer versions you can change this. For Mathematica, uses UnitStep[0]=1, and Heaviside(0)=1/2 it's just another convention: the convention of taking ( f(x+)+f(x-) )/ 2 for finite jump discontinuities.

Best regards.
Alvaro.

Thanks Alvaro.

True: only Mathcad recognizes Heaviside as a function
However, Smath proceeds the convolution integral alright.




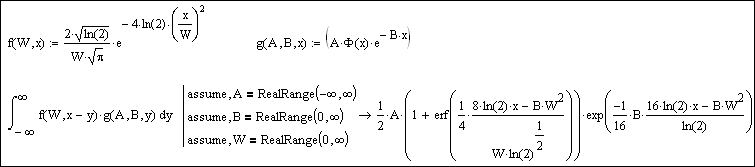
Convolution Numerical [WORKING model].sm (33 КиБ) скачан 66 раз(а).
Convolution Numerical [Unsolved MCD] Copy.sm (243 КиБ) скачан 61 раз(а).